Рене Декарт

Сочинения

Cм. курс истории философии.

К оглавлению. - Номер страницы перед текстом на ней.

ПРАВИЛА ДЛЯ РУКОВОДСТВА УМА

ПРАВИЛО I

Целью научных занятий должно быть направление ума таким образом, чтобы он мог выносить твердые и истинные суждения обо всех тех вещах, которые ему встречаются.

Таково обыкновение людей, что всякий раз, когда они замечают какое-либо сходство между двумя вещами, они в своих суждениях приписывают обеим даже в том, чем эти вещи различаются, то, что, как они узнали, является истинным для одной из них. Так, неудачно сравнивая науки, которые целиком заключаются в познании, присущем духу, с искусствами, которые требуют некоторого телесного упражнения и расположения, и видя, что один человек не в состоянии разом обучиться всем искусствам, но легче становится лучшим мастером тот, кто упражняется лишь в одном из них (ведь одни и те же руки не могут приспособиться к возделыванию земли и игре на кифаре или ко многим различным занятиям подобного рода столь же легко, как к одному из них), они думали то же самое и о науках и, отличая их друг от друга сообразно различию их предметов, полагали, что надо изучать каждую науку в отдельности, отбросив все прочие. В этом они безусловно обманывались. Ведь, поскольку все науки являются не чем иным, как человеческой мудростью, которая всегда пребывает одной и той же, на какие бы различные предметы она ни была направлена, и поскольку она перенимает от них различие не большее, чем свет солнца - от разнообразия вещей, которые он освещает, не нужно полагать умам какие-либо границы [1], ибо познание одной истины не удаляет нас от открытия другой, как это делает упражнение в одном искусстве, но, скорее, тому способствует. И право, мне кажется удивительным, что многие люди дотошнейшим образом исследуют свойства растений, движения звезд, превращения металлов и предметы дисциплин, подобных этим, но при всем том почти никто не думает о здравом смысле или об этой всеобщей мудрости, тогда как все другие вещи в конце концов следует ценить не столько ради них самих, сколько потому, что они что-то прибавляют к этой мудрости. И оттого не без основания мы вы-

ставляем это правило первым среди всех, ибо ничто так не отклоняет нас от прямого пути разыскания истины, как если мы направляем наши занятия не к этой общей цели, а к каким-либо частным. Я говорю не о дурных и достойных осуждения целях, каковыми являются пустая слава или бесчестная нажива: ведь очевидно, что приукрашенные доводы и обманы, приноровленные к способностям толпы, открывают к этим целям путь гораздо более короткий, чем тот, который может потребоваться для прочного познания истинного. Но я разумею именно благородные и достойные похвалы цели, так как они часто вводят нас в заблуждение более изощренно, как, например, когда мы изучаем науки, полезные для житейских удобств или доставляющие то наслаждение, которое находят в созерцании истинного и которое является почти единственным в этой жизни полным и не омраченным никакими печалями счастьем. Конечно, мы можем ожидать от наук этих законных плодов, но, если мы во время занятий помышляем о них, они часто становятся причиной того, что многие вещи, которые необходимы для познания других вещей, мы упускаем или потому, что они на первый взгляд кажутся малополезными, или потому, что они кажутся малоинтересными. И надо поверить в то, что все науки связаны между собой настолько, что гораздо легче изучать их все сразу, чем отделяя одну от других. Итак, если кто-либо всерьез хочет исследовать истину вещей, он не должен выбирать какую-то отдельную науку: ведь все они связаны между собой и друг от друга зависимы; но пусть он думает только о приумножении естественного света разума, не для того, чтобы разрешить то или иное школьное затруднение, но для того, чтобы в любых случаях жизни разум (intellectus) предписывал воле, что следует избрать, и вскоре он удивится, что сделал успехи гораздо большие, чем те, кто занимался частными науками, и не только достиг всего того, к чему другие стремятся, но и превзошел то, на что они могут надеяться.

ПРАВИЛО II

Нужно заниматься только теми предметами, о которых наши умы очевидно способны достичь достоверного и несомненного знания.

Всякая наука есть достоверное и очевидное познание, и тот, кто сомневается во многих вещах, не более сведущ, чем тот, кто о них никогда не думал, но при этом первый кажется более несведущим, чем последний, если о некоторых вещах он составил ложное мнение; поэтому лучше не заниматься вовсе, чем заниматься предметами настолько трудными, что, будучи не в состоянии отличить в них истинное от ложного, мы вынуждены допускать сомнительное в качестве достоверного, ибо в этих случаях надежда на приумножение знания не так велика, как риск его убавления. И таким образом, этим положением мы отвергаем все те познания, которые являются лишь правдоподобными, и считаем, что следует доверять познаниям только совершенно выверенным, в которых невозможно усомниться. И как бы ни убеждали себя ученые в том, что существует крайне мало таких познаний, ибо они вследствие некоего порока, обычного для человеческого рода, отказывались размышлять о таких познаниях как слишком легких и доступных каждому, я, однако, напоминаю, что их гораздо больше, чем они полагают, и что их достаточно для достоверного доказательства бесчисленных положений, о которых до этого времени они могли рассуждать только предположительно; и поскольку они считали недостойным ученого человека признаться в своем незнании чего-либо, они настолько привыкли приукрашивать свои ложные доводы, что впоследствии мало-помалу убедили самих себя и, таким образом, стали выдавать их за истинные.

Но если мы будем строго соблюдать это правило, окажется очень немного вещей, изучением которых можно было бы заняться. Ибо вряд ли в науках найдется какой-либо вопрос, по которому остроумные мужи зачастую не расходились бы между собой во мнениях. А всякий раз, когда суждения двух людей об одной и той же вещи оказываются противоположными, ясно, что по крайней мере один из них заблуждается или даже ни один из них, по-видимому, не обладает знанием: ведь если бы доказательство одного было достоверным и очевидным, он мог бы так изложить его другому, что в конце концов убедил бы и его разум. Следовательно, обо всех вещах, о которых существуют правдоподобные мнения такого рода, мы, по-видимому, не в состоянии приобрести совершенное знание, поскольку было бы дерзостью ожидать от нас самих большего, чем дано другим; так что, если мы правильно рассчитали, из уже открытых наук остаются только арифметика и геометрия, к которым нас приводит соблюдение этого правила.

Мы, однако, не осуждаем ввиду этого тот способ философствования, который дотоле изобрели другие, и орудия правдоподобных силлогизмов, чрезвычайно пригодные для школьных баталий, ибо они упражняют умы юношей и развивают их посредством некоего состязания, и гораздо лучше образовывать их мнениями такого рода, даже если те очевидно являются недостоверными, поскольку служат предметом спора между учеными, чем предоставлять их, незанятых, самим себе. Ведь, может быть, без руководителя они устремились бы к пропасти, но, пока они идут по следам наставников, пусть и отступая иногда от истинного, они наверняка избрали путь во всяком случае более безопасный по той причине, что он уже был изведан более опытными людьми. И мы сами рады, что некогда точно так же были обучены в школах, но поскольку мы уже освободились от клятвы, привязывавшей нас к словам учителя, и наконец в возрасте достаточно зрелом убрали руку из-под его ферулы, если мы всерьез хотим сами установить себе правила, с помощью которых мы поднялись бы на вершину человеческого познания, то среди первых, конечно, следует признать это правило, предостерегающее, чтобы мы не злоупотребляли досугом, как делают многие, пренебрегая всем легким и занимаясь только трудными вещами, о которых они искусно строят поистине изощреннейшие предположения и весьма правдоподобные рассуждения, но после многих трудов наконец слишком поздно замечают, что лишь увеличили множество сомнений, но не изучили никакой науки.

Теперь же, так как мы несколько ранее сказали, что из других известных дисциплин только арифметика и геометрия остаются не тронутыми никаким пороком лжи и недостоверности, то, чтобы более основательно выяснить причину, почему это так, надо заметить, что мы приходим к познанию вещей двумя путями, а именно посредством опыта или дедукции. Вдобавок следует заметить, что опытные данные о вещах часто бывают обманчивыми, дедукция же, или чистый вывод одного из другого, хотя и может быть оставлена без внимания, если она неочевидна, но никогда не может быть неверно произведена разумом, даже крайне малорассудительным. И мне кажутся малополезными для данного случая те узы диалектиков, с помощью которых они рассчитывают управлять человеческим рассудком, хотя я не отрицаю, что эти же средства весьма пригодны для других нужд. Действительно, любое заблуждение, в которое могут впасть люди (я говорю о них, а не о животных), никогда не проистекает из неверного вывода, но только из того, что они полагаются на некоторые малопонятные данные опыта или выносят суждения опрометчиво и безосновательно.

Из этого очевидным образом выводится, почему арифметика и геометрия пребывают гораздо более достоверными, чем другие дисциплины, а именно поскольку лишь они одни занимаются предметом столь чистым и простым, что не предполагают совершенно ничего из того, что опыт привнес бы недостоверного, но целиком состоят в разумно выводимых заключениях. Итак, они являются наиболее легкими и очевидными из всех наук и имеют предмет, который нам нужен, поскольку человек, если он внимателен, кажется, вряд ли может в них ошибиться. Но потому не должно быть удивительным, если умы многих людей сами собой скорее предаются другим искусствам или философии: ведь это случается, поскольку каждый смелее дает себе свободу делать догадки о вещи темной, чем об очевидной, и гораздо легче предполагать что-либо в каком угодно вопросе, нежели достигать самой истины в одном, каким бы легким он ни был.

Теперь из всего этого следует заключить не то, что надо изучать лишь арифметику и геометрию, но только то, что ищущие прямой путь к истине не должны заниматься никаким предметом, относительно которого они не могут обладать достоверностью, равной достоверности арифметических и геометрических доказательств.

ПРАВИЛО III

Касательно обсуждаемых предметов следует отыскивать не то, что думают о них другие или что предполагаем мы сами, но то, что мы можем ясно и очевидно усмотреть или достоверным образом вывести, ибо знание не приобретается иначе.

Следует читать книги древних, поскольку огромным благодеянием является то, что мы можем воспользоваться трудами столь многих людей как для того, чтобы узнать о тех вещах, которые уже некогда были удачно открыты, так и для того, чтобы напомнить себе о тех остающихся во всех дисциплинах вещах, которые еще надлежит придумать. Но при всем том есть большая опасность, как бы те пятна заблуждений, которые возникают из-за слишком внимательного чтения этих книг, случайно не пристали к нам, сколь бы мы тому ни противились и сколь бы осмотрительными мы ни были. Ведь писатели обычно бывают

такого склада ума. что всякий раз, когда они по безрассудному легковерию склоняются к выбору какого-либо спорного мнения, они всегда пытаются изощреннейшими доводами склонить нас к тому же; напротив, всякий раз, когда они по счастливой случайности открывают нечто достоверное и очевидное, они никогда не представляют его иначе как окутанным различными двусмысленностями, либо, надо думать, опасаясь, как бы не умалить достоинства открытия простотой доказательства, либо потому, что они ревниво оберегают от нас неприкрытую истину.

Так вот, хотя бы все они были искренними и откровенными и никогда не навязывали нам ничего сомнительного в качестве истинного, но всё излагали по чистой совести, однако, поскольку вряд ли одним человеком было сказано что-нибудь такое, противоположное чему не было бы выдвинуто кем-либо другим, мы всегда пребывали бы в нерешительности, кому из них следует поверить. И совершенно бесполезно подсчитывать голоса, чтобы следовать тому мнению, которого придерживается большинство авторов, так как, если дело касается трудного вопроса, более вероятно, что истина в нем могла быть обнаружена скорее немногими, чем многими. Но хотя бы даже все они соглашались между собой, их учение все же не было бы для нас достаточным: ведь, к слову сказать, мы никогда не сделались бы математиками, пусть даже храня в памяти все доказательства других, если бы еще по складу ума не были способны к разрешению каких бы то ни было проблем, или философами, если бы мы собрали все доводы Платона и Аристотеля, а об излагаемых ими вещах не могли бы вынести твердого суждения: ведь тогда мы казались бы изучающими не науки, а истории.

Кроме того, напомним, что никогда не следует смешивать вообще никакие предположения с нашими суждениями об истине вещей. Это замечание имеет немаловажное значение: ведь нет более веской причины, почему в общепринятой философии еще не найдено ничего столь очевидного и достоверного, что не могло бы привести к спору, чем та, что ученые, не довольствуясь познанием вещей ясных и достоверных, сперва осмелились высказаться и о вещах темных и неведомых, которых они коснулись посредством только правдоподобных предположений; затем они сами мало-помалу прониклись полным доверием к ним и, без разбора смешивая их с вещами истинными и очевидными, в конце концов не смогли заключить ничего, что не казалось бы зависимым от какого-либо положения такого рода и потому не было бы недостоверным.

Но чтобы далее нам не впасть в то же самое заблуждение, рассмотрим здесь все действия нашего разума, посредством которых мы можем прийти к познанию вещей без всякой боязни обмана, и допустим только два, а именно интуицию и дедукцию [2].

Под интуицией я подразумеваю не зыбкое свидетельство чувств и не обманчивое суждение неправильно слагающего воображения, а понимание (conceptum) ясного и внимательного ума, настолько легкое и отчетливое, что не остается совершенно никакого сомнения относительно того, что мы разумеем, или, что то же самое, несомненное понимание ясного и внимательного ума, которое порождается одним лишь светом разума и является более простым, а значит, и более достоверным, чем сама дедукция, хотя она и не может быть произведена человеком неправильно, как мы отмечали ранее [3]. Таким образом каждый может усмотреть умом, что он существует, что он мыслит, что треугольник ограничен только тремя линиями, а шар - единственной поверхностью и тому подобные вещи, которые гораздо более многочисленны, чем замечает большинство людей, так как они считают недостойным обращать ум на столь легкие вещи.

Впрочем, чтобы ненароком не смутить кого-либо новым употреблением слова "интуиция" и других слов, в использовании которых я в дальнейшем вынужден подобным же образом отдаляться от их общепринятого значения 4, я здесь вообще предупреждаю, что я совсем не думаю о том, каким образом все эти слова употреблялись в последнее время в школах, поскольку было бы очень трудно пользоваться теми же названиями, а подразумевать совершенно другое; я обращаю внимание только на то, что означает по-латыни каждое такое слово, чтобы всякий раз, когда не хватает подходящих выражений, я мог вложить нужный мне смысл в те слова, которые кажутся мне наиболее пригодными для этого.

Однако же эта очевидность и достоверность интуиции требуется не только для высказываний, но также и для каких угодно рассуждений. Взять, к примеру, такой вывод: 2 и 2 составляют то же, что 3 и 1; тут следует усмотреть не только то, что 2 и 2 составляют 4 и что 3 и 1 также составляют 4, но вдобавок и то, что из этих двух положений с необходимостью выводится и это третье.

Впрочем, может возникнуть сомнение, почему к интуиции мы добавили здесь другой способ познания, заключающийся в дедукции, посредством которой мы постигаем все то, что с необходимостью выводится из некоторых других достоверно известных вещей. Но это нужно было сделать именно так, поскольку очень многие вещи, хотя сами по себе они не являются очевидными, познаются достоверно, если только они выводятся из истинных и известных принципов посредством постоянного и нигде не прерывающегося движения мысли, ясно усматривающей каждую отдельную вещь; точно так же мы узнаем, что последнее звено какой-либо длинной цепи соединено с первым, хотя мы и не можем обозреть одним взором глаз всех промежуточных звеньев, от которых зависит это соединение, - узнаем, если только мы просмотрели их последовательно и помнили, что каждое из них, от первого до последнего, соединено с соседним. Итак, мы отличаем здесь интуицию ума от достоверной дедукции потому, что в последней обнаруживается движение, или некая последовательность, чего нет в первой, и, далее, потому, что для дедукции не требуется наличной очевидности, как для интуиции, но она, скорее, некоторым образом заимствует свою достоверность у памяти. Вследствие этого можно сказать, что именно те положения, которые непосредственно выводятся из первых принципов, познаются в зависимости от различного их рассмотрения то посредством интуиции, то посредством дедукции, сами же первые принципы - только посредством интуиции, и, напротив, отдаленные следствия - только посредством дедукции [5].

Эти два пути являются самыми верными путями к знанию, и ум не должен допускать их больше - все другие надо отвергать, как подозрительные и ведущие к заблуждениям; однако это не мешает нам поверить, что те вещи, которые были открыты по наитию, более достоверны, чем любое познание, поскольку вера в них, как и всякая вера в загадочные вещи, является действием не ума, а воли, и, если бы она имела основания в разуме, их прежде всего можно и нужно было бы отыскивать тем или другим из уже названных путей, как мы, быть может, когда-нибудь покажем более обстоятельно.

ПРАВИЛО IV

Для разыскания истины вещей необходим метод. Смертными владеет любопытство настолько слепое, что часто они ведут свои умы по неизведанным путям без всякого основания для надежды, но только для того, чтобы проверить, не лежит ли там то, чего они ищут; как если бы кто загорелся настолько безрассудным желанием найти сокровище, что беспрерывно бродил бы по дорогам, высматривая, не найдет ли он случайно какое-нибудь сокровище, потерянное путником. Точно так же упражняются почти все химики, большинство геометров и немало философов; я, правда, не отрицаю, что они иногда блуждают до такой степени удачно, что находят нечто истинное, однако я признаю по этой причине не то, что они более усердны, а лишь то, что они более удачливы. Но гораздо лучше никогда не думать об отыскании истины какой бы то ни было вещи, чем делать это без метода: ведь совершенно несомненно, что вследствие беспорядочных занятий такого рода и неясных размышлений рассеивается естественный свет и ослепляются умы; и у всех тех, кто привык таким образом бродить во мраке, настолько ослабляется острота зрения, что впоследствии они не могут переносить яркого света; это подтверждается и на опыте, так как очень часто мы видим, что те, кто никогда не утруждал себя науками, судят о встречающихся вещах гораздо более основательно и ясно, чем те, кто все свое время проводил в школах. Под методом же я разумею достоверные и легкие правила, строго соблюдая которые человек никогда не примет ничего ложного за истинное и, не затрачивая напрасно никакого усилия ума, но постоянно шаг за шагом приумножая знание, придет к истинному познанию всего того, что он будет способен познать.

Здесь же следует отметить два пункта: не принимать безусловно ничего ложного за истинное и достигать познания всех вещей, ибо если мы не знаем какую-либо вещь из тех, которые мы можем знать, то лишь потому, что мы никогда не замечали никакого пути, который вел бы нас к такому познанию, или потому, что мы впали в противоположное заблуждение. Но если метод правильно объясняет, каким образом следует пользоваться интуицией ума, чтобы не впасть в заблуждение, противное истине, и каким образом следует отыскивать дедуктивные выводы, чтобы прийти к познанию всех вещей, то, мне кажется, для того чтобы он был совершенным, не нужно ничего другого, поскольку невозможно приобрести никакого знания, кроме как посредством интуиции ума или дедукции, как уже было сказано раньше. Ведь он не может простираться и до того, чтобы указывать, каким образом следует совершать эти действия, ибо они являются первичными и

самыми простыми из всех, так что, если бы наш разум не мог пользоваться ими уже раньше, он не воспринял бы никаких предписаний самого метода, сколь бы легки они ни были. Другие же действия ума, которыми диалектика силится управлять с помощью этих двух первых, здесь бесполезны, или, скорее, их нужно отнести к числу препятствий, так как невозможно прибавить к чистому свету разума ничего, что бы некоторым образом его не помрачило.

Поскольку же польза от этого метода столь велика, что предаваться без него наукам, кажется, скорее вредно, чем полезно, я легко убеждаюсь в том, что он был некоторым образом постигнут уже прежде более сильными умами, хотя бы под руководством одной лишь природы. Ведь человеческий ум заключает в себе нечто божественное, в чем были посеяны первые семена полезных мыслей, так что часто, как бы они ни были попираемы и стесняемы противными им занятиями, они все-таки производят плод, вызревающий сам собой. Это мы замечаем в самых легких из наук - арифметике и геометрии; в самом деле, для нас достаточно ясно, что древние геометры применяли некий анализ, который они распространяли на решение всевозможных проблем, хотя и ревниво утаили его от потомков. И теперь процветает некий род арифметики, называемый алгеброй, который осуществляет в отношении чисел то, что древние делали в отношении фигур. Однако эти две науки являются не чем иным, как появившимися сами собой плодами, вызревшими из врожденных начал данного метода, и я не удивляюсь, что применительно к простейшим предметам этих наук они до сих пор развивались более успешно, чем в остальных науках, где их обычно стесняют большие препятствия, но все-таки и там, если их пестовать с величайшей заботливостью, они, без сомнения, смогут достичь полной зрелости.

Это я главным образом и задумал сделать в данном трактате: ведь я не ценил бы высоко эти правила, если бы они были достаточны только для разрешения тех пустых проблем, которыми привыкли развлекаться досужие счетчики или геометры, ибо я в этом случае полагал бы, что я выделился не чем иным, как тем, что забавлялся пустяками, быть может, более искусно, нежели другие. И хотя здесь я буду много говорить о фигурах и числах, поскольку ни из каких других дисциплин не могут быть почерпнуты примеры столь же очевидные и столь же достоверные, тем не менее всякий, кто будет внимательно следить за моей

мыслью, легко заметит, что ни о чем я не думаю здесь так мало, как об общепринятой математике, но излагаю некую другую дисциплину, такую, что упомянутые науки являются скорее ее покровом, нежели частями. Ведь эта наука должна содержать в себе первые начала человеческого рассудка и достигать того, чтобы извлекать истины из какого угодно предмета; и, если говорить откровенно, я убежден, что она превосходит любое другое знание, переданное нам людьми, так как она служит источником всех других знаний. О покрове же я сказал не потому, что хотел бы укрыть и укутать эту науку, чтобы уберечь ее от толпы, но скорее потому, что хотел бы принарядить и украсить ее так, чтоба она могла быть более приемлемой для человеческого ума.

Когда я впервые направил ум на математические дисциплины, я сразу же перечитал большую часть из того, что обычно передается от авторитетов в этих науках; в особенности я чтил арифметику и геометрию, поскольку, как было сказано, это простейшие из наук, являющиеся как бы путями к остальным. Но ни в той, ни в другой мне тогда, пожалуй, не попались в руки авторы, которые бы меня вполне удовлетворили. Конечно же очень многое из того, что я прочитал у этих авторов касательно чисел, было истинным, как я, проведя расчеты, убедился на опыте; касательно же фигур многое они определенным образом представляли моим глазам и выводили на основании некоторых заключений, но почему это обстояло именно так и каким образом было обнаружено, сами они, по-видимому, не показывали уму достаточно хорошо. Поэтому я не был удивлен, что даже многие из даровитых и образованных людей, испробовав эти науки, или быстро бросали их, как ребяческие и пустые, или, напротив, у самого порога отвращались от изучения тех же самых наук, как крайне трудных и запутанных. И действительно, нет ничего более бессмысленного, чем заниматься голыми числами и воображаемыми фигурами, так что может показаться, будто мы желаем найти успокоение в познании подобных пустяков, и потом настолько предаться тем поверхностным доказательствам, которые обнаруживаются чаще благодаря случаю, чем искусству, и относятся больше к зрению и воображению, чем к разуму, что мы некоторым образом отучимся пользоваться самим рассудком. В то же время нет ничего более сбивающего с толку, нежели посредством такого способа доказательства освобождаться от новых трудностей, скрытых в путанице чисел. Когда же потом я

подумал, откуда же повелось, что некогда первые создатели философии не хотели допускать к изучению мудрости кого-либо несведущего в математике, как будто эта дисциплина казалась им самой легкой из всех и совершенно необходимой для того, чтобы просветить и подготовить умы к освоению других, более возвышенных наук, я вполне утвердился в подозрении, что они знали некую математику, весьма отличную от общепринятой математики нашего времени. Не то чтобы я считал, что они знали эту самую науку в совершенстве, ведь их безумные ликования и жертвы, приносимые в благодарность за незначительные открытия, ясно показывают, насколько они были безыскусны. И меня не заставят отказаться от моего мнения некоторые их механизмы, которые восхваляются у историков, ибо, хотя эти механизмы, вероятно, были весьма просты, их легко можно было превозносить, вплоть до признания их чудесами, невежественной и склонной к изумлению толпе. Но я убежден, что какие-то первые семена истин, которые присущи человеческим умам от природы и которые мы в себе заглушаем, ежедневно читая и слыша о стольких различных заблуждениях, обладали в той безыскусной и незатейливой древности такою силой, что благодаря тому самому свету ума, при посредстве которого люди видели, что следует предпочитать добродетель удовольствию, а честное - полезному, даже если они а не знали, почему это обстояло именно так, они также познали истинные идеи философии и математики, хотя и не могли еще овладеть в совершенстве самими науками. И мне по крайней мере кажется, что какие-то следы этой истинной математики обнаруживаются еще у Паппа и Диофанта, которые жили пусть и не в самую раннюю эпоху, но все же за много веков до нашего времени [6]. Я поверил бы тому, что ее впоследствии утаили с неким опасным коварством сами авторы; ведь подобно тому, что многие мастера делали, как стало известно, со своими изобретениями, авторы, возможно, опасались, что эта наука, поскольку она была самой легкой и простой, обесценилась бы, став общедоступной, и вместо нее предпочли показать нам как результаты своей науки, чтобы удивить нас, кое-какие бесплодные истины, остроумно доказанные на основании умозаключений, вместо того чтобы учить самой науке, которая не оставила бы никаких поводов для удивления. Наконец, было несколько даровитейших мужей, которые в наше время попытались воскресить эту самую математику, ибо ничем другим, кажется, не является та наука, ко-

торую называют чужеземным именем "алгебра", если бы только она могла быть освобождена от множества чисел и от необъяснимых фигур, которыми она загромождена, таким образом, что не испытывала бы больше недостатка в той высшей ясности и легкости, какая должна быть, как мы предполагаем, в истинной математике. Когда эти мысли обратили меня от частных занятий арифметикой и геометрией к некоему общему исследованию математики, я прежде всего задался вопросом, что же именно подразумевают все под этим названием и почему не только уже упомянутые науки, но также астрономия, музыка, оптика, механика и многие другие называются частями математики. В данном случае, конечно, недостаточно рассмотреть происхождение названия, ибо, если бы слово "математика" означало лишь то же самое, что и "дисциплина", (все прочие) дисциплины назывались бы математическими с не меньшим правом, чем сама геометрия. Но мы видим, что нет почти ни одного человека, который, если он успел хотя бы ступить на пороги школ, не сумел бы легко различить среди встречающихся ему вещей, что же относится к математике, а что - к другим дисциплинам. Рассматривающему это более внимательно стало бы в конце концов ясно, что к математике относятся лишь все те вещи, в которых исследуются какой-либо порядок или мера, и неважно, в числах ли, или фигурах, или звездах, или звуках, в любом ли другом предмете придется отыскивать такую меру; а потому должна существовать некая общая наука, которая, не будучи зависимой ни от какого частного предмета, объясняла бы все то, что может быть обнаружено в связи с порядком и мерой, и эта самая наука должна называться не заимствованным именем, а уже сделавшимся старым, но вновь вошедшим в употребление именем всеобщей математики, ибо в ней содержится все то, благодаря чему другие науки и называются частями математики [7]. Насколько же она превосходит в полезности и легкости другие, подчиненные ей науки, видно из того, что она распространяется на все те вещи, на которые распространяются и они, и, сверх того, на многие другие, и, если она заключает в себе какие-то трудности, точно такие же обнаруживаются и в этих науках, которым вдобавок присущи и другие трудности, вытекающие из их частных предметов и ей не свойственные. Отчего же теперь, когда все узнали ее название и понимают, даже не уделяя ей внимания, чем она занимается, происходит так, что многие усердно постигают другие дисциплины, которые от нее

зависят, но саму ее никто не старается изучить? Я, конечно, удивился бы этому, если бы не знал, что все считают ее слишком легкой, и если бы не заметил уже давно, что человеческие умы, пренебрегая тем, что, как они полагают, можно легко (обнаружить), всегда спешат прямо к новым и более внушительным предметам.

Но, сознавая свою слабость, я решил в поисках знания о вещах твердо придерживаться такого порядка, чтобы, всегда начиная с самых простых и легких вещей, никогда не переходить к другим до тех пор, пока мне не покажется, что в самих этих вещах не осталось более ничего из того, к чему следует стремиться. Вот почему, насколько было в моих силах, я до сих пор разрабатывал эту всеобщую математику так, чтобы потом я мог считать себя способным изучать несколько более возвышенные науки с усердием, отнюдь не преждевременным. Однако, прежде чем отойти от этого, я попытаюсь собрать воедино и расположить по порядку все то, что я нашел весьма достойным внимания в предшествующих занятиях, как для того, чтобы впредь, когда с возрастом ослабеет память, я без труда мог, если потребует необходимость, восстановить это по своей книжке, так и для того, чтобы отныне, освободив память от этих вещей, я мог обратить более свободный ум к другому.

ПРАВИЛО V

Весь метод состоит в порядке и расположении тех вещей, на которые надо обратить взор ума, чтобы найти какую-либо истину. Мы будем строго придерживаться его, если шаг за шагом сведем запутанные и темные положения к более простым, а затем попытаемся, исходя из усмотрения самых простых, подняться по тем же ступеням к познанию всех прочих.

В одном этом заключается итог всего человеческого усердия, и для желающего приступить к познанию вещей следование данному правилу не менее необходимо, чем нить для Тесея, желающего проникнуть в лабиринт. Однако многие или не размышляют над тем, что оно предписывает, или вовсе не знают его, или предполагают, что в нем нет нужды, и часто исследуют труднейшие вопросы настолько беспорядочно, что кажутся мне поступающими точно так же, как если бы они попытались одним прыжком преодолеть расстояние от самой нижней части до верха какого-то здания, пренебрегая ступенями лестницы,

предназначенными для этой цели, или не замечая их. Так поступают все астрологи, которые, не зная природы небес и даже не понаблюдав как следует за их движениями, надеются, что они смогут определить их воздействия. Так ведет себя большинство тех людей, которые изучают механику отдельно от физики и наугад изготовляют новые орудия, приводящие в движение. Таким же образом поступают и те философы, которые, пренебрегая опытами, думают, что истина выйдет из их собственного мозга, словно Минерва из головы Юпитера.

И все они очевидно грешат против этого правила. Но так как зачастую порядок, который здесь требуется, является настолько темным и запутанным, что не все будут в состоянии узнать, каков же он, то вряд ли кто-либо сможет достаточно хорошо оградить себя от заблуждения, если он не будет тщательно соблюдать то, что излагается в следующем правиле.

ПРАВИЛО VI

Для того чтобы отделять самые простые вещи от запутанных и исследовать их по порядку, необходимо в каждом ряде вещей, в котором мы прямо вывели некоторые истины из других, усматривать, что в нем является наиболее простым и насколько удалено от этого все остальное - более, или менее, или одинаково.

Хотя и кажется, что это положение не научает ничему особо новому, оно тем не менее содержит главный секрет искусства, и во всем данном трактате нет положения более полезного: ведь оно указывает, что все вещи могут быть выстроены в некие ряды, хотя и не постольку, поскольку они относятся к какому-либо роду сущего, подобно тому как философы распределили их по своим категориям, но поскольку одни из них могут быть познаны на основании других так, что всякий раз, когда возникнет какое-либо затруднение, мы сможем тотчас узнать, не будет ли полезным сначала обозреть некоторые другие вещи, и какие именно, и в каком порядке.

Для того же, чтобы это могло быть сделано правильно, необходимо отметить, во-первых, что все вещи в том смысле, в каком они могут быть полезными для нашего замысла, согласно которому мы не рассматриваем их природы как обособленные, но сравниваем их друг с другом, чтобы познать одни на основании других, можно назвать или абсолютными, или относительными.

Абсолютным я называю все, что заключает в себе искомую чистую и простую природу, например все то, что рассматривается как независимое, причина, простое, всеобщее, единое, равное, подобное, прямое и другое в том же роде. Я называю абсолютное также самым простым и самым легким для того, чтобы пользоваться им для разрешения вопросов.

Относительным же является то, что причастно той же самой природе или по крайней мере чему-либо производному от нее, в соответствии с чем оно может быть соотнесено с абсолютным и выведено из него посредством некоего ряда, но вдобавок оно привносит в свое понятие нечто другое, что я именую отношениями; таковым (т.е. относительным) является все то, что называют зависимым, действием, сложным, частным, множественным, неравным, несходным, непрямым и т.д. Эти относительные вещи отдалены от абсолютных тем больше, чем больше они содержат подобных отношений, подчиненных друг другу; и мы предупреждаем в данном правиле, что необходимо различать все эти отношения и следить за их взаимной связью и их естественным порядком, так чтобы, начав с последнего из них, мы смогли, пройдя через все другие, достичь того, что является наиболее абсолютным.

И секрет всего искусства состоит в том, чтобы среди всех вещей мы старательно подмечали наиболее абсолютное. Ведь некоторые вещи с одной точки зрения более абсолютны, чем другие, но, будучи рассмотрены иначе, оказываются более относительными; так, всеобщее, конечно, более абсолютно, нежели частное, потому что оно обладает более простой природой, но оно же может быть названо и более относительным, нежели частное, так как в своем существовании зависит от единичных вещей и т.д. Подобным же образом некоторые вещи иногда действительно более абсолютны, чем другие, но тем не менее они еще не являются наиболее абсолютными из всех; так, если мы рассматриваем единичные вещи, вид представляет собой нечто абсолютное, если же рассматриваем род, вид есть нечто относительное; среди измеримых вещей протяжение есть нечто абсолютное, но среди протяжений таковым является длина и т.д. И наконец, для того чтобы было более понятно, что мы рассматриваем здесь ряды вещей, подлежащих познанию, а не природу каждой из них, мы намеренно перечислили причину и равное среди абсолютных вещей, хотя их природа в действительности относительна: ведь причина и действие у философов являются

соотносительными; однако, если мы здесь отыскиваем, каково действие, сначала надлежит познать причину, а не наоборот. Равные вещи также соответствуют друг другу, но те, которые являются неравными, мы узнаём лишь путем сопоставления с равными, а не наоборот и т.д.

Следует отметить, во-вторых, что существует хотя бы несколько чистых и простых природ, которые можно усмотреть прежде всего и сами по себе, независимо от каких-то других, либо в самих опытах, либо с помощью некоего присущего нам света; и мы говорим, что необходимо старательно подмечать их, ибо они являются теми же самыми природами, которые мы называем наиболее простыми в каждом ряде. Все же прочие могут быть постигнуты не иначе, как если будут выведены из них, и это осуществимо либо непосредственно и ближайшим путем, либо только через посредство двух, или трех, или более того различных заключений, число которых также необходимо заметить, чтобы узнать, на большее или на меньшее число ступеней отдалены они от первого и наиболее простого положения. Таковой является повсюду связь следствий, из коей возникают те ряды искомых вещей, к которым необходимо свести любой вопрос, чтобы он мог быть исследован при помощи верного метода. Но так как нелегко обозреть их все и, кроме того, так как их нужно не столько удерживать в памяти, сколько различать благодаря некоей остроте ума, следует отыскать нечто способное настроить умы таким образом, чтобы всякий раз, когда понадобится, они тотчас замечали их; для этого, конечно, нет, как испытал я сам, ничего более подходящего, чем приучиться с известной проницательностью размышлять обо всем самом малом из того, что мы уже восприняли ранее.

Наконец, в-третьих, следует отметить, что не нужно начинать занятия с исследования трудных вещей, но, прежде чем приступить к разрешению каких-либо определенных вопросов, сначала надлежит без всякого разбора собрать обнаруживающиеся сами собой истины и затем постепенно рассмотреть, можно ли вывести из них какие-либо другие, а из последних - опять-таки другие, и далее в той же последовательности. Потом, сделав это, необходимо внимательно поразмыслить над открытыми истинами и тщательно обдумать, почему мы смогли отыскать одни из них скорее и легче, чем другие, и каковы они, чтобы, исходя из этого, мы также могли, когда займемся каким-либо определенным вопросом, решить, к отысканию каких других истин полезно приступить прежде всего.

Например, если бы мне представилось, что число 6 есть удвоенное 3, я искал бы затем удвоенное 6, а именно 12, и снова искал бы, если угодно, удвоенное 12, а именно 24, и удвоенное 24, а именно 48, и т.д.; и отсюда я, как это нетрудно сделать, вывел бы, что между 3 и 6 существует та же самая пропорция, которая существует между 6 и 12, а также между 12 и 24 и т.д., и ввиду этого числа 3, 6, 12, 24, 48 и т.д. являются непрерывно пропорциональными. Потому-то, хотя бы все это было настолько очевидным, что показалось бы чуть ли не ребяческим, я, внимательно поразмыслив, конечно, понимаю, каким образом запутываются все вопросы, которые могут быть поставлены касательно пропорций или отношений вещей, и в каком порядке они должны быть исследованы; в одном этом заключается свод всей чисто математической науки.

Действительно, я замечаю, во-первых, что удвоенное б найти было не труднее, чем удвоенное 3, и равным образом во всех случаях, когда найдена пропорция между двумя какими бы то ни было величинами, можно допустить бесчисленное множество других величин, между которыми была бы та же самая пропорция, и что природа затруднения не изменилась бы, если бы отыскивались три, или четыре, или большее число величин подобного рода, так как, разумеется, следует искать каждую из них в отдельности, не принимая в расчет прочие. Затем я замечаю, что, хотя для данных величин 3 и 6 я легко нашел бы третью в непрерывной пропорции, а именно 12, тем не менее для двух данных крайних величин, а именно 3 и 12, не так легко можно найти среднюю, а именно 6; для рассматривающего причину этого очевидно, что здесь налицо иной род затруднения, совершенно отличный от предшествующего, так как для того, чтобы найти среднее пропорциональное, следует одновременно обращать внимание на две крайние величины и на пропорцию, которая существует между этими двумя, с тем чтобы путем ее деления получить некую новую величину; это действие весьма отлично от того, которое, если даны две величины, требуется для нахождения третьей в непрерывной пропорции. Я иду еще дальше и исследую, одинаково ли легко для данных величин 3 и 24 можно было бы найти одну из двух средних пропорциональных, а именно 6 и 12; и здесь встречается еще один род затруднения, более запутанный, чем предыдущие, ибо здесь следует одновременно обращать внимание не только на один или на два, а на три различных члена, чтобы найти четвертый. Можно пойти еще дальше и рассмотреть, было

ли бы еще труднее, если даны только 3 и 48, найти одно из трех средних пропорциональных, т.е. 6, 12 и 24; на первый взгляд кажется, что это именно так. Но потом сразу же оказывается, что это затруднение можно расчленить и уменьшить, а именно если сначала отыскивать лишь одно среднее пропорциональное - между 3 и 48, т.е. 12, а потом отыскивать другое среднее пропорциональное - между 3 и 12, а именно 6, и другое - между 12 и 48, а именно 24, и, таким образом, это затруднение можно свести ко второму, ранее описанному роду затруднения.

Из всего этого мне вдобавок видно, как можно достичь познания одной и той же вещи различными путями, один из которых гораздо труднее и темнее другого. Так, найти эти четыре непрерывно пропорциональных числа 3, 6, 12, 24, если из них допускаются два следующих друг за другом, а именно 3 и 6, или 6 и 12, или 12 и 24, с тем чтобы на основании этих двух найти остальные, будет действием чрезвычайно легким для выполнения; и тогда мы говорим, что искомая пропорция исследуется прямо. Если же допускаются два числа, чередующиеся через одно, а именно 3 и 12 или 6 и 24, с тем чтобы потом найти остальные, тогда мы говорим, что затруднение исследуется косвенно первым способом. Равным образом, когда допускаются два крайних числа, а именно 3 и 24, с тем чтобы на основании их отыскать промежуточные 6 и 12, тогда пропорция будет исследоваться косвенно вторым способом. Точно так же я мог бы продолжать и далее и вывести из одного этого примера многие другие следствия, но и упомянутых достаточно для того, чтобы читатель понял, что я хотел сказать, когда называл какое-либо положение выводимым прямо или косвенно, и чтобы он признал, что на основе знания о некоторых наиболее легких и первичных вещах многое и в других дисциплинах может быть открыто внимательно размышляющими и тщательно исследующими людьми.

ПРАВИЛО VII

Чтобы придать науке полноту, надлежит все, что служит нашей цели, вместе и по отдельности обозреть в последовательном и нигде не прерывающемся движении мысли и охватить достаточной и упорядоченной энумерацией.

Соблюдение того, что здесь предлагается, необходимо, чтобы отнести к числу достоверных те истины, которые, как мы сказали выше, непосредственно невыводимы из первых и самоочевидных принципов. Ведь это иногда делается при помощи столь длинного ряда выводов, что, когда мы достигаем данных истин, нам нелегко припомнить весь путь, который привел нас к этому; потому мы и говорим, что слабость памяти нужно возместить неким последовательным движением мысли. Так, если, например, посредством различных действий я узнал прежде всего, каковым является отношение между величинами А и В, потом между В и С, затем между С и D и, наконец, между D и Е, я не вижу еще, каково отношение между А и Е, и не могу вполне понять его на основании уже известных отношений, если не вспомню их все. Вот почему я несколько раз пробегаю их неким последовательным движением мысли, созерцающей каждое отношение в отдельности и одновременно переходящей к другим, пока не научусь переходить от первого к последнему настолько быстро, что, не допуская почти никакого участия памяти, смогу, по-видимому, созерцать всё сразу: ведь таким образом не только оказывается помощь памяти, но еще и преодолевается медлительность ума, и в некотором отношении расширяются его способности.

Однако мы добавляем, что это движение нигде не должно прерываться, так как те, кто пытается слишком быстро вывести что-либо из отдаленных принципов, часто не просматривают всю цепь промежуточных заключений настолько тщательно, чтобы не проскочить ненароком многих из них. Но конечно, как только пропускается нечто даже самое малое, тотчас разрывается цепь и рушится вся достоверность заключения.

Кроме того, мы говорим здесь, что энумерация требуется для придания науке полноты, ибо, хотя другие предписания способствуют разрешению очень многих вопросов, но только благодаря энумерации, каким бы вопросом мы ни занимали ум, мы всегда вынесем истинное и достоверное суждение о нем, и потому от нас совершенно ничего не ускользнет, а мы, по-видимому, будем знать что-либо обо всем.

Итак, здесь энумерация, или индукция, - это исследование всего того, что относится к какому-либо предложенному вопросу, настолько тщательное и точное, что на основании его мы можем с достоверностью и очевидностью заключить, что нами ничего не было пропущено по недосмотру [8]; так что, если искомая вещь и останется скрытой от нас после того, как мы применили эту энумерацию, мы по крайней мере станем более сведущими в том отноше-

нии, что твердо уясним: эта вещь не могла быть найдена никаким известным нам путем; и если, как часто бывает, мы случайно сумели бы обозреть все пути, которые открыты к ней людям, то можно было бы смело утверждать, что познание ее превосходит все способности человеческого ума.

Кроме того, следует отметить, что под достаточной энумерацией, или индукцией, мы разумеем только ту, благодаря которой истина выводится достовернее, чем посредством любого другого рода доказательства, за исключением простой интуиции, и всякий раз, когда какое-либо познание нельзя свести к индукции, для нас, если сброшены все узы силлогизмов, остается этот единственный путь, к которому мы должны проявлять полное доверие. Ибо, какие бы положения мы непосредственно ни выводили одни из других, они, если бы вывод был очевиден, оказывались бы уже сведенными к подлинной интуиции. Однако, если мы выводим нечто одно из многочисленных и разрозненных положений, способности нашего разума зачастую бывают недостаточными для того, чтобы он сумел охватить их все единым взором; в таком случае разуму следует довольствоваться достоверностью этого действия. Точно так же мы не можем одним взором глаз различить все звенья какой-либо очень длинной цепи, но тем не менее, если бы мы увидели соединение каждого звена в отдельности с соседним, этого было бы достаточно, чтобы сказать, что мы также усмотрели, каким образом последнее звено соединяется с первым.

Я сказал, что это действие должно быть достаточным, потому что часто оно может быть неполноценным и, следовательно, ведущим к заблуждению. Ведь иногда, хотя бы мы и обозрели посредством энумерации многие весьма очевидные положения, тем не менее если мы упустим нечто даже самое малое, цепь разрывается и рушится вся достоверность заключения. Иногда же мы наверное охватываем энумерацией все положения, но не различаем каждое из них в отдельности, так что все они познаются нами только смутно.

Далее, эта энумерация иногда должна быть полной, иногда - раздельной, а порой от нее не требуется ни того, ни другого, потому-то и было сказано только, что она должна быть достаточной. Действительно, если бы я захотел посредством энумерации доказать, сколько родов сущностей являются телесными и каким-либо образом доступными чувствам, я не стал бы утверждать, что их сущест-

вует столько-то, и не более, если бы прежде не узнал с достоверностью, что посредством энумерации все они были охвачены мною и каждый из них был отделен от других. Однако, если я захочу тем же путем показать, что разумная душа не является телесной, нет необходимости в том, чтобы энумерация была полной, но будет достаточно, если я разом распределю все тела по нескольким группам таким образом, что докажу: разумная душа не может быть отнесена ни к одной из них. Если, наконец, я захочу показать посредством энумерации, что площадь круга больше всех площадей других фигур равного периметра, то не нужно просматривать все фигуры, но достаточно доказать это для некоторых фигур в частности, чтобы посредством индукции вывести то же самое и для всех других.

Я добавил также, что энумерация должна быть упорядоченной, как потому, что против уже перечисленных недостатков нет никакого более действенного средства, чем исследовать все по порядку, так и потому, что, если бы, как часто случается, каждую из вещей, относящихся к обсуждаемому предмету, потребовалось рассмотреть в отдельности, не хватило бы никакой человеческой жизни, либо оттого, что эти вещи чрезвычайно многочисленны, либо оттого, что одни и те же вещи слишком часто оказывались бы подлежащими повторению. Но если мы расположим их все в наилучшем порядке, так что большинство их окажется сведенным в определенные классы, будет достаточно либо рассмотреть тщательно один из этих классов, или что-нибудь одно из каждого класса, или некоторые из них прежде, чем прочие, либо по крайней мере никогда ничего не просматривать без пользы дважды. Это полезно настолько, что зачастую благодаря правильно установленному порядку за короткое время и без особого труда доводится до конца многое, казавшееся на первый взгляд необъятным.

Однако этот порядок вещей, подлежащих энумерации, в большинстве случаев может быть различным и зависит от выбора каждого, и потому, чтобы удачно придумать его, стоит вспомнить, что было сказано в пятом правиле. Даже в самых незамысловатых человеческих искусствах есть весьма много вещей, весь метод обнаружения которых заключается в установлении этого порядка: так, если бы вы захотели составить наилучшую анаграмму посредством перестановки букв какого-либо имени, не нужно ни переходить от более легкого к более трудному, ни отличать абсолютное от относительного, ведь этим действиям

здесь нет места, но вам будет достаточно установить такой порядок исследования перестановок букв, при котором одни и те же перестановки никогда не просматривались бы дважды и совокупность их, например, была бы подразделена на определенные классы таким образом, чтобы тотчас становилось ясно, в каком именно классе больше надежды обнаружить то, что отыскивается, ведь тогда работа часто будет не долгой, а лишь ребяческой. Впрочем, не нужно разделять эти три последних правила, потому что в большинстве случаев о них следует думать одновременно и все они одинаково содействуют совершенствованию метода; и нет большой разницы, какое из них было преподано первым, но мы вкратце объяснили их здесь, потому что в оставшейся части трактата не понадобится почти ничего другого, как только изложить в частности то, что мы охватили здесь в общем.

ПРАВИЛО VIII

Если в ряде вещей, подлежащих изучению, встретится какая-либо вещь, которую наш разум не в состоянии достаточно хорошо рассмотреть, тут необходимо остановиться и не изучать другие вещи, следующие за ней, а воздержаться от ненужного труда.

Три предшествующих правила предписывают порядок и объясняют его, настоящее же указывает, когда именно он совершенно необходим и когда - только полезен. Разумеется, все, что составляет целую ступень в этом ряде, посредством которого следует переходить от относительного к чему-то абсолютному или обратно, с необходимостью нужно исследовать прежде всего дальнейшего. Но если, как часто бывает, многие вещи относятся к одной и той же ступени, всегда полезно при этом обозреть их все по порядку. Однако мы не обязаны соблюдать это требование столь точно и строго, и в большинстве случаев, хотя мы познаём с очевидностью не все, но лишь немногие вещи или даже какую-либо одну, все же можно продвигаться дальше.

Это правило с необходимостью следует из доводов, приведенных для обоснования второго правила, однако не следует считать, что оно не содержит ничего нового для того, чтобы сделать нас более учеными, хотя и кажется лишь удерживающим нас от исследования некоторых вещей и не выявляющим никакой истины: несомненно, что оно по крайней мере не учит новичков ничему другому, как

100

только тому, чтобы они не трудились понапрасну, почти на том же основании, что и второе правило. Но тем, кто вполне усвоил семь предыдущих правил, оно указывает, каким образом они смогут удовлетворить самих себя в какой угодно науке настолько, что не пожелают больше ничего; ибо всякий, кто точно соблюдал бы предыдущие правила для разрешения какого-либо затруднения и кому тем не менее будет предписано этим правилом где-либо остановиться, узнает тогда с достоверностью, что он не сможет найти искомое знание никакими стараниями, и не по причине ущербности ума, но потому, что этому препятствует природа самого затруднения или человеческий удел. Данное познание есть наука в не меньшей мере, чем то, которое выявляет природу самой вещи, и, по-видимому, не был бы в здравом уме тот, кто простирал бы свою любознательность дальше.

Все это следует пояснить одним или двумя примерами. Если, например, кто-либо занимавшийся одной лишь математикой отыскивает ту линию, которую в диоптрике называют анакластической, т.е. ту, на которой параллельные лучи преломляются таким образом, что после преломления все они пересекутся в одной точке, он, конечно, легко заметит, что в соответствии с правилами пятым и шестым определение этой линии зависит от отношения углов преломления к углам падения; но так как он не будет способен к этому исследованию, поскольку оно относится не к математике, а к физике, тут он будет вынужден остановиться на пороге и не делать ничего, если бы даже он захотел почерпнуть это знание у философов или заимствовать его из опыта: ведь он погрешил бы против третьего правила. И кроме того, это положение еще является составным и относительным, однако можно обладать достоверным опытом только в отношении вещей совершенно простых и абсолютных, как будет сказано в своем месте. Тщетно будет он также предполагать между такими углами некое соотношение, которое, по его допущению, будет самым истинным из всех, ведь тогда он скорее отыскивал бы не анакластическую линию, но лишь такую, которая бы соответствовала смыслу его предположения.

Если же какой-либо человек, который не только изучает математику, но и желает, в соответствии с первым правилом, отыскать истину во всех встречающихся вещах, натолкнется на то же самое затруднение, он обнаружит далее, что названное соотношение между углами падения и преломления зависит от изменения этих углов

101

вследствие различия сред, что это изменение опять-таки зависит от способа, каким луч проникает сквозь прозрачное тело, и что познание этого способа проникновения требует, чтобы природа действия света также была известна, что, наконец, для понимания действия света необходимо знать, что такое естественная сила вообще, и понимать, что последняя является наиболее абсолютным во всем данном ряде. Итак, после того как он ясно постигнет это посредством интуиции ума, он вернется по тем же ступеням, согласно пятому правилу, и если на второй ступени он не сможет тотчас же познать природу действия света, он перечислит, по правилу седьмому, все другие естественные силы, так что на основе познания чего-либо другого, по крайней мере посредством сравнения, о котором мы скажем позднее, он уразумеет также и эту природу; сделав это, он отыщет, каким образом луч проникает сквозь прозрачное тело, и так будет просматривать по порядку остальное, пока не дойдет до самой анакластической линии. Хотя до сих пор ее тщетно отыскивали многие, тем не менее я не вижу ничего, что могло бы препятствовать ее очевидному познанию кем-либо в полной мере использовавшим наш метод.

Но приведем самый замечательный пример. Если кто-то поставит своей задачей исследовать все истины, для познания которых достаточно человеческого разумения, - а это, мне кажется, надлежит сделать хотя бы раз в жизни всем, кто серьезно доискивается здравого смысла, - он наверняка обнаружит с помощью данных правил, что ничего невозможно познать прежде, чем разум, так как от него зависит познание всего остального, а не наоборот; затем, постигнув все то, что непосредственно следует за познанием чистого разума, он среди прочего перечислит все другие орудия познания, какими мы обладаем, кроме разума; их окажется только два, а именно фантазия и чувство. Итак, он приложит все старание, чтобы различить и исследовать три этих способа познания, и, увидя, что истина и ложь в собственном смысле могут существовать не иначе как лишь в разуме, но зачастую они ведут свое происхождение только от двух других способов, он постарается обратить внимание на все те вещи, которыми он может быть введен в заблуждение, с тем чтобы остерегаться их, и точно перечислит все пути, которые открыты людям к истине, с тем чтобы следовать верным путем: ведь они не настолько многочисленны, чтобы нельзя было легко найти их все посредством достаточной энумерации.

102

Неопытным это покажется удивительным и невероятным, как только в отношении каждого предмета он отличит те познания, которые лишь наполняют или украшают память, от тех, благодаря которым кто-либо должен быть назван поистине более просвещенным, что достигается так же легко... Он вполне осознает, что больше не пребывает в неведении относительно чего-либо по недостатку ума или умения и что другим человеком вообще не может быть познано что-нибудь, чего и он не был бы также способен познать, стоит ему как подобает направить ум на то же самое. И хотя зачастую могут предвидеться многие затруднения, исследование которых будет ему запрещено настоящим правилом, но, поскольку он ясно поймет, что эти затруднения превышают все способности человеческого ума, он не будет вследствие этого считать себя более несведущим, но само знание о том, что искомая вещь не может быть познана никем, с избытком удовлетворит его любознательность, если он благоразумен.

Но чтобы нам не быть всегда неуверенными в том, что же может познать ум, и чтобы не усердствовать неосмотрительно и понапрасну, прежде чем мы приступим к познанию вещей в частности, надлежит хотя бы раз в жизни тщательно исследовать, к каким же познаниям способен человеческий разум. Чтобы лучше осуществить это, всегда необходимо из вещей, одинаково легких, сначала исследовать те, которые являются более полезными.

Ведь этот метод подобен тем из механических ремесел, которые не нуждаются в посторонней помощи, но сами наставляют, каким образом надо изготовлять инструменты для них. Действительно, если кто-либо пожелал бы заняться одним из этих ремесел, например кузнечным, но оказался бы лишенным всех инструментов, он вначале, конечно, был бы вынужден использовать твердый камень или какую-нибудь необработанную глыбу железа вместо наковальни, взять булыжник вместо молота, приладить деревянные палки наподобие щипцов и по мере необходимости подбирать другие орудия такого же рода; затем, приготовив это, он не принялся бы тотчас же выковывать для нужд других людей мечи, или шлемы, или еще какую-нибудь вещь из тех, которые делаются из железа, но прежде всего изготовил бы молоты, наковальню, щипцы и прочие полезные для него самого инструменты. Данный пример убеждает нас в том, что, поскольку в этих начинаниях мы сможем обнаружить только некоторые безыскусные предписания, которые кажутся скорее врожденными

103

нашим умам, чем приобретенными при посредстве искусства, не следует тотчас пытаться с их помощью уладить споры философов или распутать хитросплетения математиков; но сначала их следует использовать для того, чтобы с величайшим усердием разыскивать все другое, являющееся более необходимым для исследования истины, в особенности потому, что нет никакой причины, по которой покажется более трудным раскрыть это, чем какие-либо вопросы из тех, что обычно ставятся в геометрии, или физике, или других дисциплинах.

Но здесь поистине не может быть ничего полезнее, чем изучать, что такое человеческое познание и как далеко оно простирается. Потому ныне мы и охватываем это одним-единственным вопросом, который, как мы полагаем, необходимо исследовать первым из всех при помощи правил, уже изложенных ранее, а это хотя бы раз в жизни должно быть сделано каждым из тех, кто мало-мальски любит истину, потому что в исследовании данного вопроса заключены верные средства познания и весь метод. Напротив, ничто не кажется мне более нелепым, чем, как делают многие, смело спорить о тайнах природы, о влиянии небес на эти низшие области, о предсказании грядущих событий и о подобных вещах, никогда, однако, даже не задавшись вопросом о том, достаточно ли человеческого разумения, чтобы это раскрыть. И не должно казаться утомительным или трудным делом определение границ того ума, который мы осознаем в нас самих, раз мы зачастую не колеблемся выносить суждение даже о тех вещах, которые находятся вне нас и совершенно чужды нам. И не является непомерной задачей, если мы хотим объять мыслью все вещи, содержащиеся в нашей вселенной, с тем чтобы узнать, каким образом каждая из них подлежит исследованию нашего ума: ведь не может быть ничего столь многочисленного или разрозненного, что его нельзя было бы посредством той энумерации, о которой мы говорили, заключить в известные границы и распределить по нескольким разделам. Для того же, чтобы опробовать это на предложенном вопросе, мы сначала разделяем на две части все, что его касается, так как он должен быть отнесен или к нам, способным к познанию, или к самим вещам, которые могут быть познаны; два этих пункта мы обсуждаем по отдельности.

104

И мы, конечно, замечаем в самих себе, что только разум способен к науке, но ему могут содействовать или препятствовать три другие способности, а именно воображение, чувство и память. Следовательно, нужно рассмотреть по порядку, для того чтобы остеречься, в чем каждая из этих способностей может мешать или, чтобы воспользоваться всеми их возможностями, в чем может быть полезной. И таким образом, эта первая часть будет исследована посредством достаточной энумерации, как будет показано в следующем правиле.

Затем нужно перейти к самим вещам, которые должны рассматриваться лишь постольку, поскольку они затрагиваются разумом; в этом смысле мы разделяем их на природы наиболее простые и сложные, или составные. Простые могут быть только духовными, или телесными, или относящимися и к тому и к другому роду; наконец, из составных одни разум сознает пребывающими именно таковыми до того, как он вынесет о них определенное суждение, другие же составляет он сам. Все это будет подробнее изложено в двенадцатом правиле, где будет доказано, что ложь не может иметь места нигде, кроме как в этих последних, которые составляются разумом; потому мы разделяем их еще на те, которые выводятся из простейших и самоочевидных природ и о которых мы будем рассуждать во всей следующей книге, и те, которые предполагают также другие (являющиеся, как мы убеждаемся на опыте, составными в действительности) и для описания которых мы предназначаем целиком третью книгу.

И во всем трактате мы, конечно, будем пытаться все пути, которые открыты людям к познанию истины, проследить столь тщательно и представить столь легкими, что всякий, кто в совершенстве изучит весь этот метод, каким бы посредственным умом он ни обладал, увидит тем не менее, что нет никаких путей, закрытых для него в большей степени, чем для других людей, и что он не останется больше в неведении о чем-либо по недостатку ума или умения. Но всякий раз, как он направит ум на познание какой-либо вещи, он или полностью обретет это познание, или доподлинно узнает, что оно зависит от какого-нибудь опыта, который не в его власти, и потому не станет обвинять свой ум, хотя и будет вынужден на этом остановиться, или, наконец, докажет, что искомая вещь превышает все способности человеческого ума, и, таким образом, он не будет вследствие этого считать себя более несведущим, так как знание этого является знанием в не меньшей степени, чем знание чего бы то ни было другого.

105

ПРАВИЛО IX

Следует целиком обратить взор ума на самые незначительные и наиболее легкие вещи и дольше задерживаться на них, пока мы не приучимся отчетливо и ясно усматривать истину.

Описав два действия нашего разума - интуицию и дедукцию, которыми, как мы сказали, только и надо пользоваться при изучении наук, продолжим в этом и следующем правилах разъяснение того, какими стараниями мы можем стать более способными к осуществлению этих действий и одновременно усовершенствовать две главные способности ума, а именно проницательность в отчетливом усмотрении каждой из вещей и находчивость в искусном выведении одних из других.

При этом, как нужно пользоваться интуицией ума, мы узнаем хотя бы из сравнения ее со зрением: ведь тот, кто хочет сразу обозреть одним взором много предметов, не увидит отчетливо ни одного из них; и равным образом тот, кто имеет обыкновение в одном акте мышления обращать внимание сразу на многие предметы, обладает путаным умом. Однако те мастера, которые занимаются тонкой работой и привыкли со вниманием устремлять взор на отдельные точки, благодаря упражнению приобретают способность в совершенстве различать сколь угодно малые и тонкие вещи; точно так же те, кто никогда не разбрасывается мыслью сразу на различные предметы, а всегда всецело сосредоточивается на рассмотрении самых простых и легких вещей, становятся проницательными.

Тем не менее порок, общий для смертных, заключается в том, что трудное кажется им более прекрасным; и многие полагают, что они ничего не узнают, когда усматривают весьма ясную и простую причину какой-либо вещи, а между тем они восхищаются некоторыми напыщенными и выспренними рассуждениями философов, хотя они большей частью покоятся на основаниях, никем никогда не изученных в достаточной степени: поистине безрассудны те, кто считает потемки более яркими, чем свет. Напротив, следует отметить, что те, кто действительно знает, с одинаковой легкостью распознают истину независимо от того, вывели они ее из простого предмета или из запутанного: ведь они постигают любую истину посредством сходного, единого и определенного акта, с тех пор как они однажды достигли ее; но вся разница заключается в пути, который, конечно, должен быть длиннее, если он ведет к истине, более удаленной от первых и в высшей степени безусловных начал.

106

Итак, всем следует привыкнуть сразу охватывать мыслью столь немногое и столь простое, что они никогда не сочтут себя знающими то, что не усматривается ими так же отчетливо, как то, что они познают отчетливее всего. Правда, некоторые рождаются гораздо более способными к этому, чем другие, однако при посредстве искусства, а также упражнения умы могут стать гораздо более способными к этому; есть один пункт, на который, как мне кажется, здесь следует указать прежде всего, а именно: чтобы каждый твердо убедил себя в том, что не из внушительных и темных вещей, а лишь из легких и более доступных должны выводиться сколь угодно сокровенные знания.

Ведь если я, например, захочу исследовать, может ли какая-либо естественная сила в одно мгновение перенестись в отдаленное место через все промежуточное расстояние, я не обращу ум тотчас же ни к магнитной силе, ни к влиянию звезд, ни даже к скорости света, чтобы выяснить, не происходят ли, возможно, такие действия мгновенно: ведь это может быть доказано мною с большим трудом, чем то, что требуется; но я лучше поразмышляю над пространственными перемещениями тел, так как во всем этом роде не может быть ничего более ощутимого. И я замечу, что камень действительно не может мгновенно передвинуться из одного места в другое, так как он является телом; сила же, подобная той, которая движет камнем, передается только мгновенно, если она в чистом виде переходит от одного носителя к другому. Например, если я приведу в движение один конец сколь угодно длинной палки, я легко пойму, что сила, благодаря которой движется эта часть палки, в то же самое мгновение с необходимостью приводит в движение также и все другие ее части, ибо в этом случае сила передается в чистом виде и не находится в каком-либо теле, как, например, в камне, посредством которого она переносится.

Таким же образом, если я захочу узнать, как из одной и той же простой причины могут одновременно проистекать противоположные действия, я не буду заимствовать у врачей лекарства, которые изгоняют одни жидкости и удерживают другие, и не буду нести вздор о Луне, будто она согревает посредством света и охлаждает посредством скрытого качества; но лучше я рассмотрю весы, на которых один и тот же груз в одно и то же мгновение поднимает одну чашу и вместе с тем опускает другую, и т.п.

107

ПРАВИЛО X

Чтобы стать находчивым, ум должен упражняться в разыскании тех вещей, которые уже были открыты другими, и при помощи метода обозревать даже самые незамысловатые изобретения людей, но в особенности те, которые объясняют или предполагают порядок.

Признаюсь, я родился с таким умом, что всегда находил величайшее удовольствие от занятий не в том, чтобы выслушивать доводы других, а в том, чтобы находить их собственными стараниями; это - единственное, что привлекало меня к изучению наук, когда я был еще молодым, и всякий раз, когда какая-либо книга сулила в заглавии новое открытие, я пробовал, прежде чем читать дальше, узнать, не достиг ли бы и я, возможно, чего-либо подобного благодаря некоей врожденной находчивости, и тщательно остерегался, как бы не лишить себя этого невинного удовольствия поспешным чтением. Это удавалось столь часто, что я наконец заметил, что я успешнее достигал истины вещей не так, как обыкновенно делают другие, т.е. не посредством путаных и проводимых вслепую изысканий и скорее благодаря случаю, нежели искусству, - на основе длительного опыта я выявил верные правила, которые немало способствуют этому и которыми я воспользовался впоследствии для установления многих других правил. И тщательно разработав таким образом весь этот метод, я убедился в том, что с самого начала следовал наиболее полезному из всех способов изучения.

Однако, так как от природы не у всех людей умы настолько склонны к исследованию вещей собственными силами, это правило указывает, что нам не надо сразу же заниматься более трудными и возвышенными вещами, но прежде следует изучить всякие легчайшие и простейшие искусства, и в особенности те, где царит больший порядок, каковыми являются искусство мастеров, которые ткут ткани и ковры, или женщин, которые вышивают либо переплетают нити, меняя узор ткани бесчисленными способами; такого же рода все игры с числами, все, что относится к арифметике, и т.п.: все эти искусства удивительно хорошо упражняют ум, если только мы обязаны их открытием не другим, а самим себе. Ведь поскольку в них не остается ничего скрытого и они всецело соответствуют способности человеческого познания, они отчетливейшим образом представляют нам бесчисленные порядки, совершенно различные между собой и тем не менее правильные, - порядки, в надлежащем соблюдении которых заключается почти вся человеческая находчивость.

108

И потому мы уведомили, что это нужно отыскивать при помощи метода, который в названных более легких искусствах обычно является не чем иным, как постоянным соблюдением порядка, либо существующего в самой вещи, либо искусно придуманного: так, если мы хотим прочесть писание, запечатленное в неизвестных письменах, мы, хотя тут не видно никакого порядка, все же представляем себе какой-то - как для исследования всех предположений, которые могут быть выдвинуты относительно отдельных знаков, или слов, или фраз, так и для расположения их таким образом, чтобы посредством энумерации мы узнали все, что из них может быть выведено. И более всего надо остерегаться, как бы не потерять попусту время, угадывая подобные вещи случайно и без помощи искусства: ведь, хотя они зачастую могут быть найдены без помощи искусства, а счастливчиками иногда, возможно, быстрее, чем другими при посредстве метода, они, однако, ослабляли бы свет ума и приучали бы к ребяческому и суетному настолько, что впоследствии ум всегда оставался бы на поверхности вещей и не мог бы проникнуть глубже. Но все же, чтобы не впасть в заблуждение тех, кто занимает мысль только важными и весьма возвышенными вещами (о каковых они после многих трудов приобретают лишь смутное знание, тогда как они стремятся к знанию глубокому), нам, стало быть, надлежит сначала упражняться в этих более легких вещах, но с помощью метода, так чтобы приучиться открытыми и знакомыми путями, будто играючи, всегда проникать в сокровенную истину вещей: ведь таким образом впоследствии мы постепенно и в короткое, сверх всякого ожидания, время почувствуем, что мы с одинаковой легкостью способны выводить из очевидных начал многие положения, которые кажутся очень трудными и запутанными.

Но некоторые, возможно, удивятся, что в этом месте, где мы исследуем, каким образом мы можем стать более способными к выведению одних истин из других, мы умалчиваем обо всех предписаниях диалектиков, при посредстве которых они рассчитывают управлять человеческим рассудком, предписывая ему некие формы рассуждения, которые приводят к заключению с такой необходимостью, что, положившись на них, рассудок, даже если он некоторым образом отлынивает от ясного и внимательного рассмотрения самого вывода, сможет тем не менее вывести

109

что-либо достоверное лишь на основании формы. Мы же заметим, что истина часто ускользает из этих уз, а те, кто ими пользуется, сами оказываются запутанными в них. С другими же это случается не так часто, и мы знаем из опыта, что всякого рода остроумнейшие софизмы почти никогда не вводили в заблуждение кого-либо, пользовавшегося лишь чистым рассудком, но обычно вводили в заблуждение самих софистов.

Поэтому, особенно остерегаясь здесь того, чтобы наш рассудок не был праздным в то время, как мы исследуем истину какой-либо вещи, отбросим эти формы, как препятствующие нашему намерению, и лучше отыщем все вспомогательные средства, благодаря которым наша мысль остается внимательной, как будет показано в дальнейшем. Но для того чтобы еще очевиднее обнаружилось, что упомянутое искусство рассуждения совершенно ничего не привносит в познание истины, следует заметить, что диалектики не могли бы составить при посредстве этого искусства ни одного силлогизма, приводящего к истинному заключению, если бы прежде они не располагали материалом для него, т.е. если бы они не знали уже раньше ту самую истину, которая выводится в этом силлогизме. Отсюда явствует, что они сами не узнают ничего нового при помощи такой формы, и потому общепринятая диалектика является совершенно бесполезной для стремящихся исследовать истину вещей, но только иногда может быть полезной для более легкого разъяснения другим уже известных доводов, ввиду чего ее нужно перенести из философии в риторику.

ПРАВИЛО XI

После того как мы усмотрели несколько простых положений, полезно, если мы выводим из них нечто иное, обозреть их в последовательном и нигде не прерывающемся движении мысли, поразмышлять над их взаимными отношениями и отчетливо представить сразу столь многие из них, сколь это возможно: ведь таким образом и наше познание становится гораздо более достоверным, и чрезвычайно расширяются способности ума.

Здесь представляется случай яснее изложить то, что было сказано нами об интуиции ума ранее, в третьем и седьмом правилах, так как в одном месте мы противопоставили ее дедукции, в другом же - только энумерации, которая, как мы определили, является заключением, выведенным из многих разрозненных вещей, простая же дедукция одной вещи из другой, как мы сказали там же, осуществляется при посредстве интуиции.

110

Это нужно было сделать именно так, потому что для интуиции ума нам необходимы два условия, а именно чтобы положение понималось ясно и отчетливо и затем чтобы оно понималось все сразу, а не в последовательности. Дедукция же, если мы думаем произвести ее так, как в третьем правиле, очевидно не может быть осуществлена вся сразу - она включает в себя некое движение нашего ума, выводящего одно из другого, и потому мы там по праву отличали ее от интуиции. Если же мы обращаемся к ней как к уже завершенной, тогда, как было сказано в седьмом правиле, она больше не означает никакого движения, но является пределом движения, и потому мы полагаем, что она обозревается посредством интуиции тогда, когда она проста и очевидна, но не тогда, когда она сложна и темна; в последнем случае мы дали ей название энумерации, или индукции, так как тогда она не может быть охвачена разумом вся сразу, но ее достоверность некоторым образом зависит от памяти, в которой должны удерживаться суждения о каждой из частей, подлежащих энумерации, с тем чтобы из них всех было выведено что-то одно.

Для разъяснения настоящего правила необходимо было провести все эти различия: ведь, после того как в девятом правиле говорилось только об интуиции ума, а в десятом - об одной лишь энумерации, настоящее правило объясняет, каким образом эти два действия настолько способствуют друг другу и являются настолько взаимодополняющими, что кажутся слившимися в одно действие благодаря некоему движению мысли, внимательно созерцающей каждую из вещей и одновременно переходящей к другим.

Мы отмечаем двоякую пользу этого, а именно: это позволяет достовернее познать заключение, о котором мы раздумываем, и делает ум более способным к тому, чтобы находить другие заключения. Ведь когда память, от которой, как было сказано, зависит достоверность заключений, охватывающих больше, чем мы можем постичь в одном акте интуиции, оказывается неустойчивой и слабой, она должна быть восстановлена и укреплена посредством этого непрерывного и повторяющегося движения мысли: так, если посредством многих действий я узнал сначала, каково отношение между первой и второй величинами, затем - между второй и третьей, потом - между третьей и четвертой и, наконец, между четвертой и пятой, то я не вижу при этом,

111

каково отношение между первой и пятой величинами, и не могу вывести его из уже известных отношений, если не вспоминаю их все; вот почему мне необходимо снова и снова обозревать их мыслью, пока я не буду переходить от первого к последнему столь быстро, что, не оставляя памяти почти никаких частей, я, буду, по-видимому, созерцать всё сразу.

Притом нет никого, кто не увидел бы, что этим способом преодолевается медлительность ума, а также расширяются его способности. Но кроме того, следует заметить, что наибольшая польза настоящего правила заключается в том, что, размышляя над взаимной зависимостью простых положений, мы приобретаем навык мгновенно различать, что является более или менее относительным и через какие ступени оно сводимо к абсолютному. Например, если я обозреваю несколько непрерывно пропорциональных величин, я буду размышлять над всем названным ниже, а именно посредством одинакового акта понимания, не более и не менее легкого, я узнаю отношение между первой и второй, второй и третьей, третьей и четвертой величинами и т.д.; но я не могу так же легко понять, какова зависимость второй величины от первой и третьей одновременно, и мне гораздо труднее понять зависимость второй от первой и четвертой и т.д. На основании этого я затем узнаю, в чем причина того, что, если даны только первая и вторая величины, я легко смогу найти третью и четвертую и т.д., а именно в том, что это осуществляется посредством отдельных и обособленных представлений. Если же даны только первая и третья величины, я не так легко узнаю среднюю величину, потому что это не может произойти иначе как посредством представления, которое одновременно включает два предшествующих представления. Если даны лишь первая и четвертая величины, мне будет еще труднее усмотреть две средние величины, потому что здесь сочетаются сразу три представления, так что вследствие этого показалось бы еще труднее найти на основании первой и пятой величин три средние величины. Но есть другая причина, в силу которой случается иначе, а именно та, что, хотя здесь соединены сразу четыре представления, они тем не менее могут быть разделены, поскольку четыре делится на другое число, так что я был бы в состоянии отыскать только третью величину на основании первой и пятой, а затем вторую - на основании первой и третьей и т.д. Тот, кто привык размышлять над этими и подобными вещами, всякий раз, когда он исследует новый вопрос, тотчас же узнает, что в этом вопросе порождает затруднение и каков простейший из всех способов (его разрешения); это служит величайшим подспорьем в познании истины.

112

ПРАВИЛО XII

Наконец, следует воспользоваться всеми вспомогательными средствами разума, воображения, чувства и памяти как для отчетливого усмотрения простых положений и для надлежащего сравнения искомых вещей с известными с целью познания первых, так и для отыскания тех вещей, которые должны сравниваться между собой таким образом, чтобы не осталась без внимания никакая Сторона человеческого усердия.

Это правило заключает все, что было сказано выше, и показывает в общем то, что нужно будет разъяснить в частности, следующим образом.

Для познания вещей нужно учитывать лишь два условия, а именно нас, познающих, и сами подлежащие познанию вещи. В нас имеется только четыре способности, которыми мы для этого можем воспользоваться, а именно разум, воображение, чувство и память. Конечно, один лишь разум способен к постижению истины, однако он должен прибегать к помощи воображения, чувства и памяти, с тем чтобы мы случайно не оставили без внимания нечто находящееся в нашем распоряжении. Что же касается вещей, достаточно исследовать три пункта, а именно: сначала то, что очевидно само по себе, затем как познается нечто одно на основании другого и, наконец, что из чего выводится. И эта энумерация кажется мне полной и не упускающей совершенно ничего из того, на что может простираться человеческое усердие.

Поэтому, обращаясь к первому пункту, я хотел бы изложить в этом разделе, что такое человеческий ум, что такое тело, как оно оформляется умом, каковы во всем составном существе способности, служащие познанию вещей, и как действует каждая из них, если бы данный раздел не казался мне слишком тесным для того, чтобы вместить все то, что должно быть предпослано, прежде чем в этих вещах истина сможет стать очевидной для всех. Ведь я всегда стремлюсь писать так, чтобы не утверждать ничего из того, что обычно побуждает к спору, кроме как предпосылая те самые доводы, которые привели меня к данному заключению и которыми, как я полагаю, можно убедить и других.

113

Но так как сейчас это невозможно, мне достаточно объяснить настолько кратко, насколько я смогу, какой способ постижения всего, что служит в нас познанию вещей, в наибольшей мере соответствует моему намерению. Не верьте, если вам угодно, что дело обстоит именно так, но что помешает вам следовать тем же самым предположениям, если выяснится, что они ничего не отнимают от истины вещей, но только делают все гораздо более ясным? Именно так в геометрии вы выдвигаете некоторые предположения о количестве, которыми никоим образом не ослабляется сила доказательств, хотя зачастую в физике вы думаете о его природе иначе.

Итак, во-первых, следует понять, что все внешние чувства, поскольку они являются частями тела, хотя мы и направляем их на объекты посредством деятельности, а именно посредством пространственного движения, все же, строго говоря, ощущают лишь посредством претерпевания, тем же самым способом, каким воск воспринимает фигуру от печати. И не надо думать, что это сказано ради аналогии, но следует понять, что внешняя фигура ощущающего тела реально изменяется объектом совершенно таким же способом, как фигура, которую образует поверхность воска, изменяется печатью. Это следует допустить не только тогда, когда мы осязаем какое-либо тело как обладающее фигурой, или твердое, или шероховатое и т.д., но и тогда, когда посредством осязания мы воспринимаем тепло или холод и т.п. Точно так же и в других чувствах, а именно: передняя непрозрачная часть глаза воспринимает таким образом фигуру, напечатленную под воздействием света, составленного из различных цветов, и наружная оболочка ушей, ноздрей и языка, непроницаемая для объекта, таким образом заимствует и новую фигуру у звука, запаха и вкуса.

Весьма полезно представить себе все это таким образом, так как ничто не воспринимается чувствами легче, чем фигура, ведь она осязается и созерцается. А то, что из этого предположения не следует ничего ложного скорее, чем из какого угодно другого, доказывается на основании того, что представление о фигуре является настолько общим и простым, что им охватывается любая чувственно воспринимаемая вещь. Например, ты можешь предположить, что цвет является всем, чем угодно, однако ты не будешь отрицать, что он является протяженным и, следовательно, обладающим фигурой. Что же окажется неприемлемым, если, остерегаясь, как бы нам не допустить бесполезно какое-либо новое сущее и опрометчиво не измыслить его,

114

мы при этом не будем отрицать все, что думали о цвете другие, а лишь отвлечемся от всего иного, кроме того, что обладает природой фигуры, и воспримем различие, которое существует между белым, голубым, красным и т.д., как различие, которое существует между этими или подобными им фигурами?

И то же самое может быть сказано обо всем, так как верно, что бесконечного множества фигур достаточно для описания всех различий между чувственно воспринимаемыми вещами.

Во-вторых, следует понять, что в то время, как внешнее чувство возбуждается объектом, фигура, какую оно воспринимает, передается некоей другой части тела, которая называется общим чувством [9], в то же самое мгновение и без реального перехода какого-либо сущего из одного места в другое: совершенно таким же способом, каким теперь, когда я пишу, я разумею, что в то же самое мгновение, когда на бумаге вычерчивается каждая из букв, в движении находится не только нижняя часть пера - в ней не может быть никакого, даже малейшего, движения, так чтобы одновременно оно не сообщалось и всему перу; и все эти различия движений обозначены в воздухе и верхней частью пера, хотя я не представляю себе ничего реального, переносимого с одного конца на другой. Кто же подумает, что между частями человеческого тела существует более слабая связь, чем между частями пера, и что проще можно придумать для описания этого?

В-третьих, следует понять, что общее чувство выполняет также роль печати, запечатлевая в фантазии, или воображении, как в воске, эти фигуры или идеи, приходящие от внешних чувств чистыми и бестелесными; эта фантазия является настоящей частью тела, причем такой величины, что разные ее части могут облекаться во множество фигур, отличных друг от друга, и обычно удерживать их довольно долго [10]; и тогда налицо именно то, что называется памятью.

115

В-четвертых, следует понять, что двигательная сила или сами нервы берут свое начало в мозгу, где находится фантазия, которой они различным образом приводятся в действие, подобно тому как общее чувство приводится в действие внешним чувством или как перо в целом движимо своей нижней частью. Этот пример также показывает, как фантазия может быть причиной многих движений в нервах; отчетливых образов этих движений она тем не менее не содержит в себе, но она обладает некоторыми другими образами, из которых могут проистекать эти движения, ведь и перо в целом движется не так, как его нижняя часть, более того, в своей большей части оно очевидно движется совершенно иначе и в обратном направлении. На основании этого нетрудно уразуметь, каким образом могут производиться все движения другими живыми существами, хотя в них и не допускается совершенно никакого познания вещей, но допускается лишь чисто телесная фантазия, и, кроме того, каким образом производятся в нас самих все те действия, которые мы совершаем без какого-либо содействия рассудка.

Наконец, в-пятых, следует понять, что та сила, посредством которой мы, собственно, и познаем вещи, является чисто духовной и отличается от тела в целом не менее, чем кровь от кости или рука от глаза; она является единственной в своем роде и либо вместе с фантазией воспринимает фигуры от общего чувства, либо прилагается к тем, какие сохраняются в памяти, либо создает новые фигуры, которые занимают воображение настолько, что часто оно бывает не в состоянии сразу воспринять идеи от общего чувства или претворить их в двигательную силу соответственно чисто телесной предрасположенности. Во всех названных случаях эта познающая сила иногда является пассивной, иногда деятельной и уподобляется то печати, то воску, что, однако, следует принимать здесь лишь за аналогию, ведь в телесных вещах не обнаруживается чего-либо совершенно подобного этой силе. И она является одной и той же силой, которая, когда она вместе с воображением направлена на общее чувство, обозначается словами "видеть", "осязать" и т.д.; когда она направлена на одно лишь воображение, как облекаемое в различные фигуры, она обозначается словом "вспоминать"; когда она направлена на воображение, как измышляющее новые фигуры, - словами "воображать" или "представлять"; когда, наконец, она действует одна - словом "понимать"; как совершается последнее действие, я изложу подробнее в своем месте. И потому

116

же сообразно этим различным функциям эта самая сила называется либо чистым разумом, либо воображением, либо памятью, либо чувством, но, строго говоря, она именуется умом, когда она то создает в фантазии новые идеи, то имеет дело с уже созданными; мы рассматриваем ее как способную к этим различным действиям, и различие между упомянутыми названиями нужно будет иметь в виду в дальнейшем. Поняв же все это таким образом, внимательный читатель легко заключит, на какую помощь от каждой способности следует рассчитывать и как далеко может простираться человеческое усердие, чтобы возместить недостатки ума.

Ведь если разум может приводиться в действие воображением или, наоборот, воздействовать на последнее; если воображение также может воздействовать на чувства посредством двигательной силы, направляя их на объекты, или, наоборот, чувства могут воздействовать на воображение, в котором они и запечатлевают образы тел, а память, по крайней мере та, которая телесна и подобна воспоминанию животных, ничем не отличается от воображения, то из этого, несомненно, следует, что, когда разум имеет дело с теми вещами, в которых нет ничего телесного или подобного телесному, он не может опираться на эти способности. Напротив, чтобы они не мешали ему, необходимо отстранить чувства и освободить воображение от всякого отчетливого впечатления, насколько это возможно. Однако если разум предпринимает исследование какой-либо вещи, могущей быть отнесенной к телу, ее как можно более отчетливая идея должна создаваться в воображении; для того чтобы удобнее было осуществить это, необходимо предъявить внешним чувствам саму вещь, которую данная идея будет представлять. Но много вещей не могут содействовать разуму в отчетливом усмотрении каждой из них. Для того же, чтобы вывести из многого, собранного вместе, что-либо одно, а это часто приходится делать, нужно отсечь от идей о вещах все, что не требует наличного внимания, с тем чтобы остальное легче было удержать в памяти; и таким образом, тогда нужно будет предъявлять внешним чувствам не сами вещи, a скорее их некие упрощенные изображения, которые, если только их достаточно для предотвращения ошибок памяти, оказываются тем более удобными, чем они проще. И всякий, кто будет соблюдать все это, не упустит, как мне кажется, совершенно ничего из того, что относится к этой части вопроса.

117

Для того чтобы перейти еще и ко второй его части и чтобы строго отличить понятия простых вещей от понятий тех вещей, которые из них составляются, и усмотреть в вещах обоих видов, где может быть ложь, с тем чтобы остеречься ее, и какие вещи могут быть достоверно познаны, с тем чтобы заниматься только ими, в этом разделе, как и в предшествующих, следует допустить некоторые положения, которые, возможно, не у всех получат признание. Однако даже если иные считают, что они являются не более истинными, чем те воображаемые орбиты, посредством которых астрономы описывают свои явления, это не важно, лишь бы с их помощью различали, какое познание о какой угодно вещи может оказаться истинным или ложным.

Итак, мы говорим, во-первых, что единичные вещи по отношению к нашему познанию следует рассматривать иначе, нежели высказываясь о них в зависимости от того, как они существуют в действительности. Ведь, если, например, мы рассмотрим какое-либо протяженное и обладающее фигурой тело, мы признаем при этом, что оно в порядке вещей является чем-то единым и простым, ибо в этом смысле оно не могло бы быть названо составленным из телесной природы, протяжения и фигуры, потому что эти части никогда не существовали отдельно друг от друга. Но по отношению к нашему разуму мы называем данное тело чем-то составленным из этих трех природ, так как мы уразумели каждую из них в отдельности, прежде чем смогли судить, что три эти природы одновременно обнаруживаются в одном и том же предмете. Вот почему, говоря здесь о вещах лишь постольку, поскольку они воспринимаются разумом, мы называем простыми только те, познание которых является столь ясным и отчетливым, что они не могут быть разделены умом на большее число познаваемых более отчетливо частей; таковы фигура, протяжение, движение и т.д.; все же остальные вещи мы представляем себе некоторым образом составленными из этих простых. Это следует понимать в столь общем смысле, чтобы не были исключены даже те вещи, которые мы иногда отвлекаем от самих простых вещей; это бывает, когда мы говорим, что фигура есть предел протяженной вещи, понимая под пределом нечто более общее, чем под фигурой, так как, разумеется, можно говорить также о пределе длительности, пределе движения и т.д. Ведь тогда, хотя обозначение предела отвлечено от фигуры, вследствие этого оно не должно, однако, казаться более простым, чем фигура; но скорее, поскольку понятие предела прилагают и к другим вещам, таким, как предел длительности или

118

движения и т.д., которые отличаются, как вещи совершенно иного рода, от фигуры, оно должно было быть отвлеченным также и от этих вещей, и потому оно является чем-то составленным из многих совершенно различных природ, к которым оно приложимо только неоднозначно.

Во-вторых, мы говорим, что те вещи, которые по отношению к нашему разуму называются простыми, являются или чисто интеллектуальными, или чисто материальными, или общими. Чисто интеллектуальными являются те вещи, которые познаются разумом при посредстве некоего врожденного света и без помощи какого-либо телесного образа. Ибо несомненно, что существуют некоторые вещи такого рода и невозможно измыслить какую-либо телесную идею, которая дала бы нам представление о том, что такое познание, сомнение, незнание, а также что такое действие воли, которое позволительно назвать волением, и тому подобное; тем не менее мы действительно познаем все это, и столь легко, что для этого нам достаточно лишь быть наделенными рассудком. Чисто материальными являются те вещи, которые познаются существующими только в телах: такие, как фигура, протяжение, движение и т.д. Наконец, общими следует называть те, которые без различия приписываются то телесным вещам, то духовным, как, например, существование, единство, длительность и тому подобное. Сюда следует отнести также те общие понятия, которые служат как бы некими узами для соединения других простых природ и на очевидности которых основывается все, что мы выводим в рассуждении. Именно таковы положения: "Две величины, равные какой-либо третьей, равны между собой"; "Две вещи, которые не могут быть отнесены к одной и той же, третьей, одинаковым образом, имеют какое-то различие и между собой" и т.д. И именно эти общие понятия могут быть познаны или чистым разумом, или разумом, созерцающим образы материальных вещей.

Впрочем, к числу этих простых природ позволительно отнести также лишенность и отрицание их, поскольку они разумеются нами, так как познание, посредством которого я усматриваю, что такое ничто, или мгновение, или покой, не менее истинно, чем то, посредством которого я разумею, что такое существование, или длительность, или движение. И данный способ понимания будет содействовать тому, чтобы мы впоследствии получили возможность сказать, что все остальные вещи, которые мы познаем, составлены из этих простых природ: так, если я вынесу суждение о том, что какая-либо фигура не находится в движении, я скажу, что моя мысль является некоторым образом составленной из фигуры и покоя, и так же о прочем.

119

В-третьих, мы говорим, что все эти простые природы известны сами по себе и никогда не заключают в себе никакой лжи. Это легко будет показано, если мы отличим ту способность разума, посредством которой он созерцает и познает вещь, от той, посредством которой он выносит суждение, утверждая или отрицая; ведь может случиться, что мы сочтем неизвестными нам те вещи, которые мы в действительности познаем (а именно если мы предположим, что в них кроме того, что мы созерцаем, или того, что мы достигаем в мышлении, есть нечто иное, скрытое от нас), и что эта наша мысль окажется ложной. По этой причине очевидно, что мы ошибемся, если решим, что нами никогда не будет полностью познана какая-либо из этих простых природ: ведь если мы достигаем умом хотя бы чего-то наименьшего в ней, что, конечно, необходимо, поскольку мы предполагаем вынести некоторое суждение о ней, из одного этого следует заключить, что мы познаем ее полностью; ибо иначе она не могла бы быть названа простой, а была бы составлена из того, что мы постигаем в ней, и того, что мы считаем нам неизвестным.

В-четвертых, мы говорим, что соединение этих простых вещей между собой является или необходимым, или случайным. Оно необходимо, когда одна вещь настолько подразумевается неким неявным способом в представлении о другой, что мы не сможем отчетливо представить себе ни ту, ни другую, если будем считать, что они отделены друг от друга: таким образом фигура связана с протяжением, движение - с длительностью, или временем, и т.д., потому что невозможно представить себе ни фигуру, лишенную всякого протяжения, ни движение, лишенное всякой длительности. Точно так же, если я говорю: "4 и 3 составляют 7", это составление является необходимым; ибо мы не представляем себе отчетливо число семь, если неким неявным способом не включаем в него чисел три и четыре. Таким же образом и все, что доказывается относительно фигур или чисел, необходимо соединено с тем, о чем это утверждается. И названная необходимость обнаруживается не только в чувственно воспринимаемых вещах, но также, например, если Сократ говорит, что он сомневается во всем, отсюда с необходимостью следует: значит, он понимает по крайней мере то, что он сомневается, и, значит, он познает, что нечто может быть истинным или ложным, и т.д.: ведь эти следствия необходимо связаны с природой сомне-

120

ния [11]. Случайным же является сочетание этих вещей, при котором они не соединяются никакой неразрывной связью, как, например, когда мы говорим: тело одушевлено, человек одет и т.д. Существует также много вещей, зачастую с необходимостью связанных между собой, которые причисляются к случайным большинством людей, не замечающих связи между ними; таково положение: "Я существую, следовательно, Бог существует", а также "Я понимаю, следовательно, обладаю умом, отличным от тела" и т.д. Наконец, следует отметить, что случайны и высказывания, обратные очень многим высказываниям, являющимся необходимыми: так, хотя из того, что я существую, я достоверно вывожу, что Бог существует, однако на основании того, что Бог существует, невозможно утверждать, что я также существую.

В-пятых, мы говорим, что мы никогда не сможем уразуметь ничего, кроме этих простых природ и некоторого их смешения, или соединения, между собой; причем зачастую легче сразу заметить многие природы, связанные между собой, чем отделить одну из них от других, ведь я, например, могу познавать треугольник, хотя бы я никогда и не думал о том, что в познании его содержится также познание угла, линии, числа три, фигуры, протяжения и т.д. Это, однако, не мешает нам говорить, что природа треугольника составлена из всех этих природ и что они являются более известными, чем треугольник, поскольку они есть то самое, что в нем разумеется; кроме того, в этом же треугольнике скрыто, возможно, и многое другое, чего мы не замечаем, как, например, величина углов, которые равны двум прямым, и бесчисленные отношения, какие существуют между сторонами и углами, и вместимость площади и т.д.

В-шестых, мы говорим, что те природы, которые мы называем составными, познаются нами или потому, что мы узнаем на опыте, каковы они есть, или потому, что мы составляем их сами. Мы испытываем все, что воспринимаем чувством, все, что слышим от других, и вообще все, что приходит к нашему разуму или извне, или вследствие созерцания, обращенного им на самого себя. Здесь следует заметить, что разум никогда не может быть введен в заблуждение никаким опытом, если он усматривает исключительно лишь ту вещь, которая является его объектом, поскольку он располагает ею или в самом себе, или в образе, и если вдобавок он не признаёт ни того, что воображение верно воспроизводит объекты чувств, ни того, что чувства воспринимают действительные фигуры вещей, ни

121

того, наконец, что внешние вещи всегда таковы, какими они кажутся. Мы подвержены заблуждению во всех следующих случаях: если кто-либо рассказал нам небылицу и мы верим, что речь шла о происшедшем событии; если страдающий желтушной болезнью считает, что все вокруг желтое, так как его глаз окрашен в желтый цвет; если, наконец, когда расстроено воображение, как это случается с меланхоликами, мы полагаем, что его беспорядочные призраки представляют действительные вещи. Однако это не введет в заблуждение разум мудреца, так как все, что он воспримет от воображения, он, конечно, будет считать действительно запечатленным в последнем, однако он никогда не признает, что одна и та же вещь переходит в целости и без какого-либо изменения от внешних вещей к чувствам и от чувств к фантазии, если прежде он не узнал об этом каким-то другим способом. Но мы сами составляем вещи, которые разумеем, всякий раз, когда мы верим, что в них содержится нечто непосредственно не воспринимаемое нашим умом ни в каком опыте: так, когда больной желтухой убеждается в том, что видимые им вещи желтые, эта его мысль будет составлена из того, что представляет ему его фантазия, и того, что он добавляет от себя, а именно: цвет кажется ему желтым не вследствие изъяна глаза, а потому что видимые им вещи действительно желтые. Отсюда следует, что мы можем обманываться только тогда, когда вещи, в которые мы верим, некоторым образом составляются нами самими.

В-седьмых, мы говорим, что это составление может быть осуществлено тремя способами, а именно: посредством внушения, посредством предположения или посредством дедукции. По внушению составляют свои суждения о вещах те, кто располагает свой ум к вере во что-либо, склоняясь к ней не на каком-то разумном основании, а только будучи побуждаем либо некоей вышней силой, либо собственной свободой, либо склонностью фантазии: первая никогда не вводит в заблуждение, вторая - редко, третья - почти всегда; но первая не имеет отношения к данному разделу, так как она не подпадает под правила искусства. Посредством предположения мы составляем суждения, как, например, когда на основании того, что вода, более удаленная от центра мира, чем земля, составляет и более тонкую субстанцию, а также того, что воздух, находящийся выше воды, является и более разреженным, чем она, мы допускаем, что выше воздуха находится нечто эфирное, наичистейшее и гораздо более тонкое, чем сам воздух, и т.д.

122

Но все, что мы составляем таким способом, хотя и не вводит нас в заблуждение (если мы считаем это только вероятным и никогда не утверждаем, что оно истинно), но и не делает нас более сведущими.

Итак, остается одна лишь дедукция, посредством которой мы сможем составлять вещи так, что будем уверены в их истине; однако и в ней может быть много недостатков: например, если из того, что в данном пространстве, наполненном воздухом, мы ничего не воспринимаем ни посредством зрения, ни посредством осязания, ни посредством какого-либо другого чувства, мы заключаем, что это пространство является пустым, неправильно соединяя природу пустоты с природой этого пространства; и так происходит всякий раз, когда мы считаем, что из отдельной или случайной вещи может быть выведено нечто общее и необходимое. Но в нашей власти избежать этой ошибки, а именно если мы никогда не будем соединять никакие предметы, не усмотрев, что соединение одного с другим является совершенно необходимым, как, например, если мы выводим, что никакая вещь, не будучи протяженной, не может обладать фигурой, из того, что фигура необходимо связана с протяжением, и т.д.

Из всего этого следует, во-первых, что мы четко и, как я думаю, посредством достаточной энумерации разъяснили то, что сначала смогли показать, лишь беспорядочно и грубо [используя оружие, врученное нам] Минервой, а именно: людям не открыто никаких других путей к достоверному познанию истины, кроме очевидной интуиции и необходимой дедукции, а также разъяснили и то, что представляют собой те простые природы, о которых говорилось в восьмом правиле. И ясно, что интуиция ума распространяется как на познание всех этих природ, а также необходимых связей между ними, так, наконец, и на все остальное, что разум прямо испытывает как находящееся или в нем самом, или в фантазии. О дедукции же больше будет сказано в дальнейшем.

Во-вторых, отсюда следует, что не нужно вкладывать никакого труда в познание этих простых природ, так как они достаточно известны сами по себе, но нужно только отделять их друг от друга и созерцать каждую в отдельности, устремляя на нее взор ума. Ведь нет настолько тупоумного человека, который не заметил бы, что, когда он сидит, он некоторым образом отличается от самого себя, стоящего на ногах; однако не все так же четко отделяют природу положения от остального, что содержится в этой мысли, и не

123

могут утверждать, что в данном случае не меняется ничего, кроме положения. Мы не зря предупреждаем здесь об этом, так как зачастую ученые бывают настолько остроумными, что найдут способ стать слепыми даже в том, что является самоочевидным и что всегда знают даже крестьяне; это случается с ними всякий раз, когда они пытаются объяснить эти известные сами по себе вещи при посредстве чего-либо более очевидного: ведь они или разъясняют другое, или не разъясняют совершенно ничего. Действительно, кто не замечает всего того, каким бы оно ни было, по отношению к чему происходит изменение, когда мы меняем место, но кто представит себе то же самое, когда ему будет сказано: место есть поверхность окружающего тела [12]? В то время как эта поверхность может изменяться, я остаюсь неподвижным и не меняющим места; или, наоборот, она может двигаться со мной так, что, хотя меня будет окружать та же самая поверхность, тем не менее я более не буду находиться в одном и том же месте. Но не кажется ли, что ученые произносят магические слова, которые имеют таинственный смысл и превосходят способности человеческого ума, когда они говорят, что движение - вещь, известнейшая каждому, - есть акт сущего в потенции, поскольку оно находится в потенции [13]? Ведь кто поймет эти слова? Кто не знает, что такое движение? И кто не признает, что они искали узлы в тростнике? Итак, следует сказать, что никогда не нужно пользоваться для объяснения вещей никакими определениями такого рода, чтобы мы не постигали составные вещи вместо простых; но каждому нужно внимательно созерцать лишь вещи, отделенные от всех других, сообразно свету своего ума.

В-третьих, из сказанного следует, что все человеческое знание заключается только в том, чтобы мы отчетливо усматривали, каким же образом эти простые природы сходятся воедино для составления других вещей. Это весьма полезно отметить, так как всякий раз, когда предполагают исследовать какое-либо затруднение, почти все останавливаются на пороге, пребывая в сомнении относительно того, какими мыслями они должны занять ум, и решив, что необходимо отыскать какой-нибудь новый род сущего, ранее им неизвестный; например, если их спрашивают, какова природа магнита, они, предчувствуя, что это вещь непростая и трудная, тотчас же отвлекают ум от всего того, что очевидно, обращают его ко всему наитруднейшему и, скитаясь, ждут, не найдут ли они случайно, блуждая в пустом пространстве многочисленных причин,

124

чего-либо нового. Но тот, кто думает, что в магните не может быть познано ничего, что не состояло бы из некоторых простых природ, известных сами по себе, и не сомневается в том, что надлежит сделать, сначала тщательно собирает все те опыты с этим камнем, какими он может располагать, затем пытается вывести из них, каково сочетание простых природ, необходимое для того, чтобы произвести все те действия, которые были опытным путем обнаружены им в магните; однажды раскрыв это, он может смело утверждать, что постиг подлинную природу магнита, насколько она могла быть раскрыта человеком на основании данных опытов.

Наконец, в-четвертых, из сказанного следует, что никакие познания вещей не нужно считать более темными, чем другие, поскольку все они одной и той же природы и заключаются лишь в составлении вещей, известных сами по себе. Почти никто этого не замечает, но, отдавая предпочтение противоположному мнению, более самонадеянные даже позволяют себе объявлять свои предположения как бы подлинными доказательствами, и в вещах, которых они совершенно не знают, они предсказывают, что словно сквозь облако узрят истины, зачастую темные; их они не боятся выставлять напоказ, облекая свои представления в те или иные слова, с помощью которых они обыкновенно много рассуждают и последовательно говорят, но которых на самом деле не понимают ни они сами, ни их слушатели. Более же скромные часто воздерживаются от исследования многих вещей, хотя и легких и весьма необходимых для жизни, только потому, что считают себя неспособными их исследовать; и так как они полагают, что эти вещи могут быть постигнуты другими, наделенными большим умом, они присоединяются к мнениям тех, чьему авторитету они больше доверяют.

В-восьмых, мы говорим, что можно только вывести либо вещи из слов, либо причину из действия, либо действие из причины, либо подобное из подобного, либо части или само целое из частей...

Впрочем, для того чтобы кто-либо случайно не упустил из виду ряд наших предписаний, мы разделяем все, что может быть познано, на простые положения и вопросы. Для простых положений мы не выдвигаем иных предписаний, кроме тех, которые подготовляют познавательную способность к более отчетливому созерцанию и более проницательному исследованию каких угодно объектов, так как эти положения должны возникать сами собой и не мо-

125

гут быть искомыми; это мы очертили в первых двенадцати правилах, в которых, как мы полагаем, мы представили все то, что, по нашему мнению, может каким-либо образом сделать более легким использование рассудка. Из вопросов же одни совершенно понятны, если даже неизвестно их решение, - мы будем говорить только о них в двенадцати правилах, непосредственно следующих за настоящим; наконец, другие не разумеются в совершенстве - их мы откладываем до последних двенадцати правил. Такое разделение мы придумали не без умысла: как для того, чтобы не быть принужденными говорить о вещах, которые предполагают познание последующего, так же и для того, чтобы с самого начала усвоить те вещи, которыми, как мы полагаем, и следует прежде всего заниматься с целью усовершенствования умов. Надо заметить, что к числу совершенно понятных вопросов мы относим только те, в которых четко различаем три вещи, а именно: по каким признакам может быть распознано то, что является искомым, когда оно встретится; что именно представляет собой то, из чего мы должны его вывести; и как должно быть доказано, что они зависят друг от друга до такой степени, что одно ни в коем случае не может измениться, если другое остается неизменным. Поскольку мы будем располагать всеми посылками, останется объяснить не что иное, как то, каким образом находят заключение хотя и не посредством выведения из одной простой вещи чего-то одного (ведь, как уже было сказано, это может быть произведено и без предписаний), но посредством выделения чего-то одного зависимого от многих соединенных вместе вещей, - выделения настолько искусного, что для него нигде не потребуется большей способности ума, чем требуется для того, чтобы сделать простейший вывод. Вопросы подобного рода, так как они в большинстве своем являются отвлеченными и встречаются почти исключительно в арифметике или геометрии, неискушенным покажутся малополезными, однако я напоминаю, что в изучении этого искусства должны дольше усердствовать и упражняться те, кто желает в совершенстве овладеть следующей частью данного метода, в которой мы рассуждаем обо всех других вопросах.

ПРАВИЛО XIII

Если мы вполне понимаем вопрос, его надо освободить от любого излишнего представления, свести к простейшему вопросу и посредством энумерации разделить на возможно меньшие части.

126

Мы подражаем диалектикам лишь в том, что, как они для обучения формам силлогизмов предполагают термины, или содержание последних, известными, так и мы здесь заранее требуем, чтобы вопрос был вполне понят. Однако мы не различаем, как они, два крайних и средний термины, а рассматриваем весь этот предмет таким образом: во-первых, во всяком вопросе с необходимостью должно быть нечто неизвестное, ибо иначе не стоило бы и задаваться им; во-вторых, само это неизвестное должно быть каким-либо способом обозначено, ибо иначе мы не были бы побуждаемы отыскивать именно его скорее, чем что-либо другое; в-третьих, оно может быть обозначено так только через посредство чего-то другого, являющегося известным. Все это есть и в несовершенных вопросах: так, если нас спрашивают, какова природа магнита, то, что, по нашему разумению, обозначается при помощи этих двух слов - "магнит" и "природа", является известным, что и побуждает нас отыскивать именно это скорее, чем другое, и т.д. Но, вдобавок, для того чтобы вопрос был совершенным, мы хотим, чтобы он был во всех отношениях определен настолько, что не отыскивалось бы ничего более, кроме того, что может быть выведено из данного: например, если кто-либо спросит у меня, какой вывод о природе магнита должен быть сделан исключительно на основании тех опытов, проведение которых приписывает себе Гильберт [14], будь они верными или неверными; а также, если меня спросят, что я думаю о природе звука исключительно лишь на основании того, что три струны А, В, С издают одинаковый звук и из них струна В по предположению вдвое толще, чем А, но не длиннее ее и натянута грузом в два раза более тяжелым, а струна С хотя и не толще, чем А, но только вдвое длиннее и вместе с тем натянута грузом в четыре раза более тяжелым, и т.д. Из этого легко понять, каким образом все несовершенные вопросы могут быть сведены к совершенным, что подробнее будет изложено в своем месте; а также видно, каким образом может быть соблюдено данное правило, чтобы освободить хорошо понятое затруднение от всякого излишнего представления и довести его до того, чтобы мы больше не помышляли заниматься тем или иным предметом, а в общем сравнивали бы друг с другом некоторые величины. Ибо после того, например, как мы решили рассмотреть лишь те или иные опыты с магнитом, для нашего мышления не будет представлять никакого затруднения отвлечься от всех других опытов.

127

Кроме того, стоит добавить, что затруднение надо сводить к простейшему, а именно согласно пятому и шестому правилам, и разделять согласно седьмому правилу: например, если я исследую магнит на основании многих опытов, я буду обозревать их по отдельности один за другим; таким же образом, если я исследую звук, то, как было сказано, я буду по отдельности сравнивать друг с другом струны А и В, потом A и С и т.д., чтобы впоследствии охватить их все вместе достаточной энумерацией. И здесь на ум приходят лишь три этих предписания, которые должны соблюдаться чистым разумом по отношению к терминам какого-либо положения, прежде чем мы дойдем до его окончательного разъяснения, если потребуется применить следующие одиннадцать правил; каким образом это надлежит сделать, станет яснее из третьей части данного трактата. Под вопросами же мы разумеем все то, в чем отыскивается истинное или ложное; их различные роды следует перечислить для того, чтобы определить, что мы в состоянии предпринять по отношению к каждому из вопросов.

Мы уже сказали, что только в интуиции вещей, либо простых, либо составных, не может быть лжи; и в этом смысле они еще не называются вопросами, но они получают такое название, как только мы решаем вынести о них какое-то определенное суждение. Ведь мы относим к числу вопросов не только те, которые исходят от других людей, но стоял вопрос также о самом незнании, или, вернее, сомнении Сократа, когда, впервые обратившись к нему, Сократ начал исследовать, не было ли истинным то, что он во всем сомневается, и убедился, что это так.

Отыскиваем же мы либо вещи на основании слов, либо причины на основании действий, либо действия на основании причин, либо целое или другие части на основании частей, либо, наконец, сразу многое из этого.

Мы говорим, что вещи отыскиваются на основании слов, всякий раз когда затруднение заключается в неясности речи; сюда относятся не только все загадки, каковой была загадка Сфинкса о живом существе, которое сначала является четвероногим, затем двуногим и потом наконец становится трехногим, а также загадка рыбаков, которые, стоя на берегу с удилищами и крючками для рыбной ловли, говорили, что у них больше нет того, что они поймали, но, наоборот, у них есть то, чего они еще не смогли поймать, и т.д. - также и большая часть того, о чем спорят ученые, почти всегда относится к вопросу о названии. И не следует

128

столь плохо думать о великих умах, полагая, что они плохо представляют себе сами вещи, всякий раз когда они объясняют их при помощи не вполне подходящих слов: например, когда они называют местом поверхность окружающего тела, они не представляют себе ничего действительно ложного, а лишь неверно употребляют слово "место", обозначающее сообразно общепринятому употреблению ту простую и известную саму по себе природу, в силу которой говорится, что нечто находится здесь или там, и которая целиком заключается в некотором отношении вещи, о коей говорится, что она находится в определенном месте, к частям внешнего пространства, - природу, которую иные, видя, что название "место" укрепилось за окружающей поверхностью, неудачно назвали внутренним "где" [15]; то же происходит и в других случаях. И эти вопросы о названии встречаются так часто, что если бы среди философов навсегда установилось согласие относительно значения слов, то почти все их споры были бы прекращены.

Причины отыскиваются на основании действий, всякий раз когда мы исследуем относительно какой-либо вещи, существует ли она, или какова она...

Впрочем, поскольку, в то время как нам предлагается разрешить какой-либо вопрос, мы зачастую не узнаем тотчас же, к какому роду он относится, и то ли надо отыскивать вещи на основании слов, то ли причины на основании действий и т.д., мне ввиду этого кажется излишним много говорить об этих предметах в отдельности. В самом деле, будет быстрее и удобнее, если мы сразу проследим по порядку все, что надлежит сделать для разрешения любого затруднения; и потому в каждом данном вопросе прежде всего надо постараться отчетливо уразуметь, что в нем отыскивается.

Ведь иные часто так торопятся в исследовании положений, что направляют на их разъяснение блуждающий ум, прежде чем узнают, по каким признакам они смогут различить искомую вещь, если та случайно встретится; они не менее глупы, чем тот мальчик, который, будучи куда-то послан хозяином, так стремился услужить, что бросился бежать, еще не получив приказаний и не зная, куда же было велено пойти.

Но безусловно, хотя во всяком вопросе и должно быть нечто неизвестное, ибо иначе не стоило бы задаваться им, все же необходимо, чтобы оно было так обозначено посредством определенных условий, что мы всецело были бы вынуждены исследовать что-то одно скорее, чем другое. И та-

129

ковыми являются условия, о которых мы говорим, что их изучением следует заняться с самого начала: это произойдет, если мы направим взор ума так, чтобы отчетливо усмотреть каждое из них, тщательно исследуя, насколько то неизвестное, которое мы отыскиваем, определяется каждым из них; ведь при этом человеческие умы обыкновенно впадают в заблуждение двояким образом, а именно или допуская нечто большее, чем то, что дано для определения вопроса, или, наоборот, нечто упуская.

Следует остерегаться, как бы не предположить большего и более точного, чем то, что дано, особенно в загадках и других вопросах, искусно придуманных для того, чтобы обводить умы, но подчас и в прочих вопросах, когда для их разрешения, по-видимому, допускается в качестве достоверного нечто, в чем нас убеждает не какой-то верный довод, а укоренившееся мнение. Например, в загадке Сфинкса не нужно думать, что названием "нога" обозначаются только настоящие ноги живых существ, но нужно еще рассмотреть, не может ли оно относиться к чему-то другому, как оно и есть, а именно к рукам ребенка и к палке старца, поскольку и тем и другим пользуются, как ногами, для передвижения. Таким же образом в загадке рыбаков нужно остерегаться, чтобы мысль о рыбах не овладела нашим умом настолько, что отвлекла бы его от представления о тех животных, которых бедняки помимо желания зачастую носят с собой и, поймав, выбрасывают. Таков же и случай, когда отыскивается, каким образом была устроена некогда виденная нами чаша, в центре которой возвышалась колонна, на коей была водружена статуя Тантала, как бы намеревающегося напиться: хотя налитая вода прекрасно держалась в этой чаше, пока не поднималась настолько высоко, что могла бы попасть в рот Тантала, однако лишь только она достигала губ несчастного, вся она тотчас же вытекала. На первый взгляд кажется, что вся хитрость заключалась в устройстве этой статуи Тантала; однако на самом деле оно никоим образом не определяет вопрос, а лишь сопутствует ему, ибо все затруднение состоит только в том, чтобы отыскать, каким образом должна быть устроена чаша, чтобы вся вода вытекала из нее, как только она достигнет определенной высоты, но никак не раньше. Точно так же, наконец, когда на основании всех тех наблюдений за звездами, которыми мы располагаем, отыскивается, что мы можем с достоверностью утверждать об их движениях, не нужно безосновательно допускать, что Земля неподвижна и помещена в центре мира, как делали древние, потому что так казалось нам с детства, но как раз это и должно быть подвергнуто сомнению, с тем чтобы впоследствии мы изучили, какое достоверное суждение можно вынести на этот счет; и так же в остальных случаях.

130

Пропусками же мы грешим всякий раз, когда не размышляем над каким-либо условием, требующимся для определения вопроса, выражено ли оно в самом вопросе или должно быть понято каким-то иным образом: например, когда отыскивается вечное движение, но не естественное, каковым является движение звезд или ключевых вод, а произведенное человеческим усердием, кто-то (коль скоро некоторые люди верили в то, что это может быть осуществлено, полагая, что Земля беспрерывно вращается вокруг своей оси, а магнит сохраняет все качества Земли) может подумать, что он откроет вечное движение, если приладит этот камень так, чтобы тот двигался по кругу или по крайней мере сообщал железу свое движение вместе с другими своими свойствами. Даже если бы это и произошло, он, однако, не произвел бы при помощи искусства вечного движения, а лишь воспользовался бы тем движением, которое является естественным, точно так, как если бы он в речном потоке расположил колесо таким образом, чтобы оно всегда находилось в движении; а значит, он упустил бы условие, требующееся для определения вопроса, и т.д.

Достаточно поняв вопрос, нужно ясно усмотреть, в чем заключается составляющее его затруднение, чтобы легче разрешить его, освободив от всего остального.

Не всегда достаточно понять вопрос для того, чтобы узнать, в чем заключено составляющее его затруднение; но вдобавок надо поразмыслить над каждой из вещей, которые являются в нем искомыми, с тем чтобы, если нам встретятся легко обнаруживаемые вещи, мы опустили их и, устранив их из обсуждаемого положения, оставили лишь то, что нам неизвестно. Так, в вопросе о чаше, описанном немногим ранее, хотя мы и легко замечаем, как должна быть сделана чаша - в ее центре должна быть воздвигнута колонна, на чаше должна быть изображена птица и т.д., - остается, когда мы отбросим все это как не относящееся к делу, затруднение в чистом виде, заключающееся в том, что вода, содержащаяся в чаше, достигнув определенной высоты, вся вытекает; нужно отыскать, отчего это происходит.

131

Итак, мы говорим здесь, что только и стоит по порядку обозреть все данное в некотором положении, отбрасывая то, что с очевидностью покажется нам не относящимся к делу, удерживая необходимое и откладывая сомнительное для более тщательного исследования.

ПРАВИЛО XIV

То же самое следует отнести к реальному протяжению тел, и протяжение в целом должно предстать воображению через посредство простых фигур, ибо таким образом оно гораздо отчетливее представляется разумом.

Для того же, чтобы воспользоваться также и помощью воображения, следует отметить, что всякий раз, когда выводится нечто неизвестное из чего-либо другого, уже заранее известного, вследствие этого не открывается какой-то новый род сущего, но все это знание лишь расширяется до такой степени, что мы представляем себе искомую вещь тем или иным способом приобщенной к природе того, что дано в положении. Например, если кто-то слеп от рождения, не надо надеяться на то, что при помощи каких-либо доводов мы когда-нибудь сделаем так, что он представит себе верные идеи цветов, какими мы обладаем, получая их от чувств; однако, если кто-то хотя бы когда-нибудь видел основные цвета, а промежуточных и смешанных не видел никогда, может быть так, что при посредстве некоей дедукции он представит образы и тех цветов, которых он не видел, на основании их сходства с другими цветами. Точно так же, если в магните обнаружится какой-либо род сущего, подобного которому дотоле не постигал наш разум, не надо надеяться на то, что мы когда-нибудь познаем его посредством рассуждения, - для этого мы должны были бы быть наделенными либо каким-то новым чувством, либо божественным умом; но мы поверим, что достигнем всего, что в этом деле может быть осуществлено человеческим умом, если мы весьма отчетливо представим себе то сочетание уже известных сущностей, или природ, которое производит те же самые действия, какие выявляются в магните.

Конечно, все эти уже известные сущности, каковыми являются протяжение, фигура, движение и им подобные, которые здесь неуместно перечислять, познаются посредством одной и той же идеи в различных предметах, и мы не представляем себе по-равному фигуру венца, будь он серебряный или золотой; эта общая идея переносится с одного предмета на другой не иначе как посредством простого сравнения, благодаря которому мы утверждаем, что искомое является в том или ином отношении подобным,

132

либо тождественным, либо равным чему-то данному, так что во всяком рассуждении мы точно познаем истину только посредством сравнения. Например, так: всякое А есть В, всякое В есть С, следовательно, всякое А есть С; сравниваются друг с другом искомое и данное, а именно А и С, соответственно тому, что и то и другое есть В, и т.д. Но, поскольку, как мы уже много раз предупреждали, формы силлогизмов никоим образом не способствуют постижению истины вещей, читателю будет полезно, полностью отбросив их, понять, что вообще все познание, которое не приобретается посредством простой и чистой интуиции какой-либо единичной вещи, приобретается посредством сравнения двух или многих вещей. И конечно, почти все усердие человеческого рассудка состоит в том, чтобы подготовлять это действие, ибо, когда оно очевидно и просто, не требуется никакой помощи искусства, а нужен только естественный свет для того, чтобы усмотреть истину, которая обретается благодаря этому сравнению. Следует отметить, что сравнения называются простыми и очевидными лишь тогда, когда искомая и данная вещи одинаковым образом приобщаются к некоторой природе; все же остальные сравнения нуждаются в подготовке не по какой другой причине, кроме как потому, что эта общая природа находится в обеих вещах не одинаковым образом, а соответственно каким-то другим отношениям или пропорциям, в которые она облекается; и особая роль человеческого усердия состоит не в чем ином, как в сведении этих пропорций к тому, чтобы стало ясно видно равенство между искомым и тем, что известно.

Далее следует отметить, что к такому равенству не может быть сведено ничего, кроме допускающего большее и меньшее, и что все это охватывается названием "величина", так что, после того как в соответствии с предшествующим правилом термины затруднения были отвлечены от любого предмета, мы понимаем, что отныне будем заниматься только величинами вообще.

Но для того чтобы и тогда воображать нечто и пользоваться не чистым разумом, а разумом, прибегающим к помощи образов, рисуемых в фантазии, следует, наконец, отметить, что о величинах вообще нельзя сказать чего-либо, что не могло бы быть отнесено и к каждой из них в отдельности.

133

Из этого легко заключить, что будет весьма полезно, если мы перенесем то, что, по нашему разумению, можно сказать о величинах вообще, на тот вид величины, который и легче и отчетливее всего рисуется в нашем воображении; а таким является реальное протяжение тел, отвлеченное от всего иного, кроме того, что оно обладает фигурой; это следует из сказанного в двенадцатом правиле, где мы представляли себе саму фантазию вместе с содержащимися в ней идеями не чем иным, как подлинно реальным, протяженным и обладающим фигурой телом. Это также очевидно само по себе, так как ни в каком другом предмете не проявляются более четко все различия пропорций; ведь, хотя одна вещь может быть названа более или менее белой, чем другая, а равно и один звук - более или менее высоким, чем другой, и т.д., мы все же не можем точно определить, состоит ли такое превышение в двойной или тройной пропорции и т.д., кроме как посредством некоторой аналогии с протяжением тела, обладающего фигурой. Следовательно, остается незыблемым и неизменным положение о том, что вполне определенные вопросы едва ли содержат в себе какое-либо затруднение, кроме того, которое заключается в выведении равенств из пропорций; и все то, в чем обнаруживается именно такое затруднение, может и должно быть с легкостью отделено от всякого другого предмета и затем сведено к протяжению и фигурам, о которых мы поэтому, оставив любую другую мысль, только и будем рассуждать далее вплоть до двадцать пятого правила.

Здесь нам хотелось бы найти читателя, склонного к занятиям арифметикой и геометрией, хотя я предпочел бы, чтобы он еще не занимался названными науками, нежели был обучен им по общему обыкновению: ведь применение излагаемых мною здесь правил в изучении этих наук, для которого оно вполне достаточно, является гораздо более легким, чем применение их в вопросах любого другого рода; и польза от этого для достижения более возвышенной мудрости столь велика, что я не побоюсь сказать, что данная часть нашего метода была открыта не благодаря математическим проблемам - скорее сами они должны изучаться почти исключительно ради совершенствования этого метода. И я не предполагаю в упомянутых дисциплинах ничего, кроме, быть может, некоторых вещей, кои известны сами по себе и доступны каждому; однако их познание, каким обычно обладают иные люди, даже если оно не искажено какими-либо явными ошибками, тем не менее затемняется многочисленными двусмысленными и неправильно понятыми принципами, что мы попытаемся в разных местах исправить в дальнейшем.

134

Под протяжением мы разумеем все то, что обладает длиной, шириной и глубиной, не рассматривая, реальное ли это тело или только пространство; и, кажется, нет нужды в более обстоятельном объяснении, ибо нет ничего, что легче представлялось бы нашим воображением. Так как, однако, ученые часто пользуются столь тонкими различениями, что рассеивают естественный свет и находят неясности даже в тех вещах, которые всегда известны и крестьянам, то их надо предупредить, что словом "протяжение" здесь не обозначается нечто отдельное и обособленное от самого предмета и что вообще мы не признаем таких философских сущностей, которые действительно были бы недоступны воображению. Ведь, хотя кто-нибудь и сумеет убедить себя, например, в том, что, если все, являющееся протяженным в природе вещей, обратится в ничто, это, однако, не окажется противоречащим тому, что будет существовать одно лишь протяжение само по себе, он тем не менее воспользуется для этого представления не телесной идеей, а только разумом, выносящим неправильное суждение. Он сам признает это, если внимательно поразмыслит над тем самым образом протяжения, который он тогда же попытается создать в своей фантазии: действительно, он заметит, что он не воспринимает его лишенным всякого предмета, а представляет себе его совершенно иначе, нежели судит о нем; так что эти отвлеченные сущности (что бы разум ни думал об истине вещей) все-таки никогда не создаются в фантазии отделенными от их предметов.

Но, так как отныне мы не будем ничего предпринимать без помощи воображения, стоит потрудиться над тем, чтобы строго различить, посредством каких идей должно быть сообщено нашему разуму каждое из значений слов. Вот почему мы предлагаем рассмотреть три следующие формы выражения: протяжение занимает место, тело обладает протяжением, и протяжение не есть тело.

Первая из них показывает, каким образом протяжение принимается за то, что является протяженным; действительно, я разумею совершенно одно и то же и когда говорю: протяжение занимает место, и когда говорю: протяженное занимает место. Из этого, однако, не следует, что во избежание двусмысленности лучше пользоваться словом протяженное, ибо оно не обозначало бы столь четко то, что мы разумеем, а именно то, что какой-либо предмет занимает место, так как он является протяженным; и кто-нибудь мог бы истолковать выражение: протяженное есть предмет, занимающий место, - только так, как если бы я сказал: одушевленное занимает место. Это рассуждение объясняет, почему мы сказали, что будем здесь вести речь скорее о протяжении, чем о протяженном, хотя мы и считаем, что протяжение не должно пониматься иначе, чем протяженное.

135

Перейдем теперь к следующим словам: тело обладает протяжением, - где мы, хотя и понимаем, что протяжение обозначает нечто иное, чем тело, тем не менее не создаем в нашей фантазии двух различных идей: одну - тела, другую - протяжения, а создаем только одну идею протяженного тела; в действительности это не что иное, как если бы я сказал: тело является протяженным, или, вернее, протяженное является протяженным. Это свойственно тем сущностям, которые пребывают только в другом и никогда не могут быть поняты без их предмета; иначе обстоит дело с теми сущностями, которые реально отличаются от их предметов, ибо если бы я, например, сказал: Петр обладает богатствами, - то идея Петра была бы совершенно отлична от идеи богатств; таким же образом, если бы я сказал: Павел богат, - я вообразил бы нечто совершенно иное, чем если бы я сказал: богатый есть богатый. Не распознавая этого различия, многие неверно полагают, что протяжение содержит в себе нечто отличное от того, что является протяженным, подобно тому как богатства Павла есть нечто иное, чем сам Павел.

Наконец, когда говорится: протяжение не есть тело, - тогда слово "протяжение" понимается совсем иначе, чем выше; и в данном значении ему не соответствует в фантазии никакая особая идея, а все это высказывание исходит от чистого разума, который один обладает способностью обособлять отвлеченные сущности такого рода. Это становится причиной заблуждения, свойственного многим людям, которые, не замечая, что протяжение, взятое в таком смысле, не может быть воспринято воображением, представляют его себе посредством верной идеи; поскольку же эта идея необходимо включает в себя понятие тела, то, когда они говорят, что протяжение, понимаемое таким образом, не есть тело, они неразумно противоречат себе самим, приходя к тому, что одна и та же вещь одновременно является и телом и не телом. И весьма важно различать высказывания, в которых такие названия, как протяжение, фигура, число, поверхность, линия, точка, единица и т.д., обладают настолько узким значением, что исключают и то, от чего они на самом деле не отличаются, как тогда, когда говорится: протяжение или фигура не есть тело; число не есть счисляемая вещь; поверхность есть предел тела, линия - поверхности, точка - линии; единица не есть количество и т.д. Все эти и подобные им положения должны быть совершенно отделены от воображения, как бы верны они ни были; вот почему мы не будем вести о них речь в дальнейшем.

136

Нужно особо отметить, что во всех других положениях, где эти названия, хотя они и сохраняют то же самое значение и признаются тем же самым способом отвлеченными от их предметов, все-таки не исключают или не отрицают что-либо, от чего они реально не отличаются, мы можем и должны воспользоваться помощью воображения, ибо тогда, хотя разум замечает исключительно лишь то, что обозначается словом, воображение все же должно создать верную идею вещи, для того чтобы, когда потребует необходимость, сам разум мог обращаться к другим ее свойствам, не выраженным в названии, и никогда не полагал опрометчиво, что они были исключены. Так, если стоит вопрос о числе, мы воображаем какой-то предмет, измеряемый посредством многих единиц, и, хотя разум в это время размышляет только о множественности данного предмета, мы тем не менее будем остерегаться, чтобы впоследствии он не пришел на основании этого к какому-либо заключению, где предполагалось бы, что счисляемая вещь была исключена из нашего представления; так делают те люди, которые приписывают числам и удивительные тайны, и сущие пустяки, в кои они, конечно, не уверовали бы до такой степени, если бы не представляли себе число отличным от счисляемых вещей. Таким же образом, если мы имеем дело с фигурой, мы будем считать, что говорим о протяженном предмете, понимаемом только в том смысле, что он обладает фигурой; если - с телом, то мы будем считать, что говорим о том же самом предмете как обладающем длиной, шириной и глубиной; если - с поверхностью, то мы представим себе его как обладающий длиной и шириной, опуская, но не отрицая глубину; если - с линией, то представим себе его только как обладающий длиной; если - с точкой, то представим себе его, опуская все иное, кроме того, что он есть сущее.

Хотя я здесь подробно обосновываю все эти выводы, умы смертных все же настолько полны предубеждений, что я еще опасаюсь, что в данной части трактата очень немногие будут достаточно надежно ограждены от всякого риска заблуждения и что в этом длинном рассуждении они найдут объяснение моего мнения слишком кратким;

137

действительно, сами науки - арифметика и геометрия, хотя они и являются наиболее достоверными из всех, тем не менее здесь вводят нас в заблуждение. Ибо какой счетчик не думает, что его числа должны быть не только отвлечены разумом от всякого предмета, но и действительно отделены от него воображением? Какой геометр не затемняет очевидность своего объекта противоречивыми принципами, когда он утверждает, что линии не имеют ширины, а поверхности - глубины, и тем не менее потом образовывает одни из других, не замечая, что та линия, в результате движения которой, по его представлению, возникает поверхность, есть настоящее тело, а та линия, которая не имеет ширины, есть только модус тела, и т.д.? Но, чтобы не задерживаться слишком долго на перечислении этих ошибок, изложим покороче, каким образом, по нашему предположению, должен пониматься наш объект, чтобы мы как можно легче доказали все истинное, что утверждается о нем в арифметике и геометрии.

Итак, мы занимаемся здесь протяженным объектом, не рассматривая в нем совершенно ничего иного, кроме самого протяжения, и умышленно воздерживаясь от употребления слова "количество", ибо некоторые философы настолько изощренны, что они отличили также количество от протяжения [16]; но мы предполагаем, что все вопросы приведены к такому виду, что не требуется ничего иного, кроме как познать некое протяжение на основании сравнения его с каким-то другим протяжением, уже известным. Действительно, поскольку мы не ожидаем здесь познания какого-нибудь нового сущего, а только хотим привести пропорции, сколь бы запутанными они ни были, к тому, чтобы неизвестное было найдено равным чему-то известному, то, несомненно, все те различия пропорций, которые существуют в других предметах, могут быть обнаружены также и между двумя или многими протяжениями. И потому для нашей цели достаточно рассмотреть в самом протяжении все те свойства, которые могут способствовать выявлению различий пропорций, и таковых оказывается только три, а именно измерение, единица и фигура.

Под измерением мы разумеем не что иное, как способ и основание, в соответствии с которыми какой-либо предмет рассматривается как измеримый, так что не только длина, ширина и глубина суть измерения тела, но и тяжесть есть измерение, в соответствии с которым предметы взвешиваются, скорость есть измерение движения, и других таких примеров бесконечное множество. Ведь само де-

138

ление на многие равные части, будь оно реальным или только мысленным, есть собственно измерение, в соответствии с которым мы исчисляем вещи; и тот способ, каким образуется число, собственно, и называется видом измерения, хотя есть некоторая разница в значениях этого слова. Действительно, когда мы рассматриваем части по отношению к целому, тогда мы говорим, что исчисляем; когда, наоборот, рассматриваем целое как разделенное на части, мы измеряем его: например, мы измеряем века годами, днями, часами и мгновениями; если же мы будем считать мгновения, часы, дни и годы, мы в конце концов дойдем и до веков.

Из этого явствует, что в одном и том же предмете может быть бесконечное множество различных измерений и что они совершенно ничего не добавляют к измеряемым вещам, но понимаются одинаковым образом, независимо от того, имеют ли они реальное основание в самих предметах или были придуманы по произволу нашего ума. Действительно, чем-то реальным является тяжесть тела, или скорость движения, или разделение века на годы и дни, но не таково разделение дня на часы и мгновения и т.д. Тем не менее все это признается одинаковым, если рассматривается только в отношении измерения, как это следует делать здесь и в математических дисциплинах, ибо исследование того, является ли основание упомянутых измерений реальным, больше касается физиков.

Рассмотрение этого обстоятельства проливает много света на геометрию, так как почти все плохо представляют в ней три вида величины: линию, поверхность и тело. В самом деле, как было отмечено ранее, линия и поверхность непредставимы как действительно отличные от тела или друг от друга, но, когда они рассматриваются просто как отвлеченные разумом, тогда они суть различные виды величины не в большей степени, чем одушевленное и живое в человеке суть различные виды субстанции. И следует заметить мимоходом, что три измерения тел - длина, ширина и глубина - отличаются друг от друга только названием, ибо ничто не мешает в каком-то данном теле избрать какое угодно протяжение в качестве длины, а другое - в качестве ширины и т.д. И хотя только эти три измерения имеют реальное основание во всякой протяженной вещи как просто протяженной, все-таки здесь мы принимаем их во внимание не более, чем бесконечное множество других измерений, которые или создаются разумом, или имеют другие основания в вещах: так, в треугольнике, если мы

139

хотим точно его измерить, необходимо в действительности знать три величины, а именно: либо три стороны, либо две стороны и один угол, либо два угла и площадь и т.д.; точно так же в трапеции необходимо знать пять, а в тетраэдре - шесть величин и т.д., которые все могут быть названы измерениями. Для того же, чтобы избрать здесь те из них, которые в наибольшей степени содействуют нашему воображению, мы никогда не будем одновременно обращать внимание больше, чем на одно или два измерения, рисуемых в нашей фантазии, даже если мы понимаем, что в положении, которым мы будем заниматься, содержится сколько угодно других. Ведь задача искусства - различать возможно большее число их так, чтобы мы замечали только очень немногие из них одновременно, но вместе с тем все - в последовательности.

Единица есть та общая природа, к которой, как мы сказали выше, должны быть одинаково приобщены все те вещи, какие сравниваются между собой. И если в вопросе нет какой-либо уже определенной единицы, мы можем взять вместо нее или одну из уже данных величин, или любую другую, которая и будет общей мерой для всех остальных; и мы поймем, что в ней заключено столько же измерений, сколько и в тех крайних членах, которые должны будут сравниваться между собой, и представим ее себе либо просто как нечто протяженное, отвлекаясь от всего иного (тогда она будет тем же самым, что и точка у геометров, когда они посредством ее движения образуют линию), либо как некоторую линию, либо как квадрат.

Что касается фигур, то выше уже было показано, как посредством их одних могут быть образованы идеи всех вещей; в данном случае нам остается уведомить, что из бесчисленного количества их различных видов мы будем использовать здесь только те, которыми наиболее легко выражаются все различия отношений или пропорций. Существует же только два рода вещей, которые сравниваются между собой: множества и величины; и для того, чтобы сделать их доступными нашему представлению, мы располагаем также и двумя родами фигур. Например, точки, которыми обозначается треугольное число, или древо, которое раскрывает чью-нибудь родословную, и т.д. являются фигурами, представляющими множество; те же фигуры, которые непрерывны и неделимы, такие, как треугольник, квадрат и т.д., представляют величины.

140

Для того же, чтобы теперь изложить, какими из всех этих фигур мы будем здесь пользоваться, необходимо знать, что все отношения, какие только могут быть между сущностями одного и того же рода, должны быть сведены к двум главным, а именно к порядку или к мере.

Кроме того, надо знать, что для нахождения порядка требуется немало усердия, как это везде можно видеть в настоящем методе, который не научает почти ничему другому; в познании же порядка, после того как он был найден, не заключается совершенно никакой трудности, но мы можем легко обозреть умом, в соответствии с седьмым правилом, каждую из упорядоченных частей, именно потому что в этом роде отношений одни части соотносятся с другими сами по себе, а не через посредство чего-то третьего, как это бывает с мерами, о развертывании которых мы здесь поэтому только и будем рассуждать. Действительно, я узнаю, каков порядок, связывающий А и В, не рассматривая ничего иного, кроме обоих крайних членов; но я не узнаю, каково соотношение по величине между двумя и тремя, если не рассмотрю нечто третье, а именно единицу, которая является общей мерой обоих чисел.

Надо также знать, что непрерывные величины с помощью принятой единицы иногда целиком могут быть сведены к множеству и всегда - по крайней мере частично, а множество единиц может быть затем расположено в таком порядке, что затруднение, которое касается познания меры, будет в конце концов зависеть лишь от рассмотрения порядка, и успеху этого искусство содействует в наибольшей степени.

Надо, наконец, знать, что из измерений непрерывной величины нет ни одного, которое представлялось бы более отчетливо, чем длина и ширина, и что не следует одновременно обращать внимание на большее число измерений в одной и той же фигуре, если мы будем сравнивать друг с другом два различных измерения, ибо требуется искусство для того, чтобы, располагая больше чем двумя различными измерениями, подлежащими сравнению друг с другом, мы последовательно обозревали их, но одновременно обращали внимание только на два из них.

141

Заметив это, легко заключить, что положения здесь должны быть отвлечены от тех самых фигур, о которых рассуждают геометры, когда вопрос стоит о них, - отвлечены не менее, чем от любой другой материи. Для этой цели не следует оставлять ничего, кроме прямолинейных и прямоугольных поверхностей или прямых линий, которые мы также называем фигурами, потому что через их посредство мы воображаем действительно протяженный предмет в не меньшей степени, нежели через посредство поверхностей, как было сказано выше. Наконец, через посредство тех же самых фигур следует представлять то непрерывные величины, то множество или число; и для того, чтобы выявить все различия отношений, человеческим усердием не может быть изобретено ничего более простого.

ПРАВИЛО XV

В большинстве случаев полезно также чертить эти фигуры и представлять их внешним чувствам для того, чтобы таким способом легче удерживать нашу мысль сосредоточенной.

А то, как следует изображать эти фигуры, чтобы, когда они находятся перед глазами, их образы отчетливее запечатлевались в нашем воображении, является самоочевидным: так, вначале мы изобразим единицу тремя способами, а именно: в виде квадрата ,

если мы сосредоточим внимание на ней как на обладающей длиной и шириной, либо в виде линии ___, если мы будем рассматривать ее только как обладающую длиной, либо, наконец, в виде точки , если мы не заметим в ней ничего иного, кроме того, что благодаря ей составляется множество; но, как бы она ни изображалась и ни понималась, мы всегда будем подразумевать, что она является предметом, вполне протяженным и вмещающим бесконечное множество измерений. Точно так же и термины положения, когда нужно одновременно сосредоточить внимание на двух их различных величинах, следует представлять в виде прямоугольника, две стороны которого будут двумя названными величинами, таким образом: , когда они несоизмеримы с единицей, либо так:

142

или так: , когда они соизмеримы с ней; и не требуется ничего более, если только не ставится вопрос о множестве единиц. Если, наконец, мы сосредоточиваем внимание только на одной из этих величин, мы начертим линию либо в виде прямоугольника, одна сторона которого будет названной величиной, а другая - единицей, таким образом: - это бывает всякий раз, когда одну и ту же линию необходимо сравнить с какой-то поверхностью; либо в виде одной лишь длины, таким образом: ___________ , если она рассматривается только как несоизмеримая длина; либо таким образом: , если она является множеством.

ПРАВИЛО XVI

Что же касается вещей, которые не требуют наличного внимания ума, хотя и необходимы для заключения, то их лучше обозначать посредством наиболее сокращенных знаков, чем посредством полных фигур, ибо тогда память не сможет ошибаться, а вместе с тем и мысль не будет отвлекаться на то, чтобы удержать их, в то время как она занята выведением других.

Впрочем, поскольку мы сказали, что из бесчисленных измерений, которые могут быть изображены в нашей фантазии, нужно созерцать одним взором глаз или ума не более двух различных измерений, то важно удерживать в памяти все остальные таким образом, чтобы они легко представлялись всякий раз, когда потребует необходимость; по-видимому, с этой целью память и была создана природой. Но так как память зачастую подвержена ошибкам, то для того, чтобы мы не были вынуждены уделять некоторую часть нашего внимания ее восстановлению, в то время когда мы заняты другими мыслями, искусство весьма кстати открыло возможность применения письменности. Полагаясь на ее помощь, мы здесь совершенно ничего не вверяем памяти, но, предоставив свободной фантазии в целом наличные идеи, изображаем на бумаге все, что должно быть сохранено, и делаем это посредством наиболее сокращенных знаков, чтобы, после того как в соответствии с девятым правилом мы рассмотрели каждый из них в отдельности, мы смогли в соответствии с одиннадцатым правилом обозреть их все в наибыстрейшем движении мысли и одновременно охватить взором наибольшее их число.

143

Итак, все, что для разрешения затруднения надлежит рассматривать как нечто единое, мы будем обозначать одним знаком, который может быть изображен как угодно. Но ради удобства мы воспользуемся буквами а, b, с и т.д. для выражения уже известных величин и А, В, С и т.д. для выражения неизвестных. Мы часто будем ставить перед ними цифры 2, 3, 4, и т.д. для того, чтобы обозначить количество этих величин; вместе с тем мы будем располагать цифры и позади них, для того чтобы обозначать число отношений, которые надлежит в них уразуметь: так, если я напишу 2а в кубе, это будет то же самое, как если бы я сказал: удвоение величины, обозначаемой буквой а и содержащей три отношения. И благодаря этому приему мы не только произведем сокращение многих выражений, но и, что особенно важно, представим термины затруднения в столь чистом и подлинном виде, что, не упуская ничего полезного, мы вместе с тем никогда не найдем в них ничего излишнего и того, что напрасно отвлечет способности ума, в то время как нужно будет одновременно охватить умом многие вещи.

Для того чтобы яснее уразуметь все это, нужно прежде всего заметить, что счетчики имели обыкновение обозначать каждую из величин посредством многих единиц или посредством какого-либо числа, мы же в данном случае отвлекаемся от самих чисел не меньше, чем несколько ранее от геометрических фигур или от любой другой вещи. Мы делаем это как для того, чтобы избежать пресыщения долгим и ненужным вычислением, так и в особенности для того, чтобы части предмета, которые имеют отношение к природе затруднения, всегда оставались раздельными и не скрывались за бесполезными числами: например, если отыскивается основание прямоугольного треугольника, данные стороны которого равняются 9 и 12, счетчик скажет, что оно равно корень из 225, или 15; мы же вместо 9 и 12 поставим а и b и найдем, что основание равно корень из (а в квадрате + b в квадрате), при этом те два члена а в квадрате и b квадрате, которые в числе являются слитыми, останутся раздельными.

Нужно также заметить, что под числом отношений надлежит понимать следующие в непрерывном порядке пропорции, которые в общепринятой алгебре иные пытаются выразить посредством многих измерений и фигур; первую из них они называют корнем, вторую - квадратом, третью - кубом, четвертую - биквадратом и т.д. Признаюсь, что эти названия долгое время вводили меня самого в заб-

144

луждение, ибо мне казалось, что после линии и квадрата моему воображению ничто не может представиться яснее, чем куб и другие фигуры, созданные по их подобию; и действительно, с помощью этих фигур я разрешил немало затруднений. Однако в конце концов после многих опытов я убедился в том, что никогда не находил благодаря этому способу понимания ничего такого, чего я не сумел бы познать гораздо легче и отчетливее и без него, а также в том, что нужно полностью отбросить такие названия, чтобы не извратить ими наше представление, ибо одна и та же величина, хотя она и называется кубом или биквадратом, тем не менее, согласно предшествующему правилу, никогда не должна представляться воображению иначе как в виде линии или поверхности. Поэтому нужно особо отметить, что корень, квадрат, куб и т.д. являются не чем иным, как непрерывно пропорциональными величинами, которым, как предполагается, всегда предпослана та принятая единица, о коей мы уже говорили выше. Первая пропорциональная величина связана с этой единицей непосредственно и одним лишь отношением, вторая же связана с ней через посредство первой и потому - двумя отношениями, третья - через посредство первой и второй и тремя отношениями и т.д. Итак, отныне мы будем называть первой пропорциональной ту величину, которая в алгебре именуется корнем, второй пропорциональной - ту, которая именуется квадратом, и т.д.

Наконец, нужно заметить, что, хотя мы отвлекаем здесь термины затруднения от некоторых чисел для того, чтобы исследовать его природу, тем не менее часто бывает так, что оно может быть разрешено более простым способом с помощью данных чисел, чем если бы оно было отвлечено от них: это происходит благодаря двойному применению чисел (которого мы уже коснулись ранее), а именно потому, что одни и те же числа раскрывают то порядок, то меру. И стало быть, после того как мы исследовали это затруднение, выраженное в общих терминах, нужно свести его к данным числам, чтобы увидеть, не наведут ли они нас тогда, быть может, на какое-то более простое решение: например, после того как мы увидели, что основание прямоугольного треугольника со сторонами а и b равно корень из a2+b2 и что вместо а2 надо поставить 81, а вместо b2 - 144, т.е. числа, дающие в сумме число 225, корень которого, или средняя пропорциональная между единицей и 225, равен 15, мы из этого узнаем, что основание 15 соизмеримо

145

со сторонами 9 и 12, но не потому, что оно вообще является основанием прямоугольного треугольника, одна сторона которого относится к другой, как 3 к 4. Все это различаем мы, стараясь обрести очевидное и отчетливое познание вещей, а не счетчики, которые, когда им попадается искомая сумма, бывают удовлетворены, даже если они не замечают, каким образом она зависит от данных чисел; однако только в этом, собственно, и заключается наука.

Вообще же следует заметить, что никогда не нужно вверять памяти какую-либо из тех вещей, которые не требуют постоянного внимания, если мы можем изложить их на бумаге, а именно для того, чтобы бесполезным воспоминанием не отвлекать какую-то часть нашего ума от познания наличного объекта. И надо составить таблицу, в которую мы запишем термины вопроса в том виде, в каком они будут изначально представлены, а затем то, каким образом они отвлекаются и посредством каких знаков выражаются, чтобы, после того как решение будет найдено в этих самых знаках, мы легко и без всякой помощи памяти применили его к частному предмету, о котором будет стоять вопрос; действительно, никогда нельзя отвлекать что-либо, кроме как от чего-то менее общего. Итак, я пишу следующим образом: в прямоугольном треугольнике ABC отыскивается основание АС, - и представляю затруднение в отвлеченном виде, чтобы вообще отыскивалась величина основания по величинам сторон; затем вместо стороны АВ, которая равна 9, я ставлю а, вместо стороны ВС, которая равна 12, я ставлю b, и т.д.

Необходимо отметить, что мы еще воспользуемся этими четырьмя правилами в третьей части настоящего трактата и будем понимать их несколько шире, чем они были истолкованы здесь, так, как будет сказано в своем месте.

ПРАВИЛО XVII

Нужно прямо обогреть предложенное затруднение, отвлекаясь от того, что какие-то его термины являются известными, а какие-то - неизвестными, и усматривая благодаря правильным рассуждениям взаимную зависимость каждого из них от других.

146

Четыре предшествующих правила указали, каким образом определенные и вполне понятые затруднения должны быть отвлечены от каждого из их предметов и приведены к такому виду, чтобы затем не требовалось ничего другого, кроме как познать некоторые величины на основании того, что они связаны тем или иным отношением с некоторыми данными. Теперь же в этих пяти следующих правилах мы изложим, каким способом те же самые затруднения должны быть преобразованы так, что, сколько бы неизвестных величин ни было в одном положении, все они будут подчинены друг другу и как первая из них будет соотноситься с единицей, точно так же и вторая будет соотноситься с первой, третья - со второй, четвертая - с третьей; таким образом, в последовательности эти величины, если они достаточно многочисленны, составят сумму, равную какой-то известной величине. И это обеспечивается методом настолько надежным, что мы таким образом твердо убеждаемся в том, что указанные величины никакими стараниями не могли быть сведены к более простым терминам.

Что же касается настоящего правила, то следует отметить, что во всяком вопросе, подлежащем разрешению посредством дедукции, есть один ровный и прямой путь, которым мы можем легче всего переходить от одних терминов к другим, все же прочие являются более трудными и окольными. Чтобы это понять, нужно вспомнить сказанное в одиннадцатом правиле, где мы разъяснили, что связь положений такова, что, сравнивая каждое из них с соседними, мы легко замечаем, каким образом соотносятся друг с другом также первое и последнее из них, даже если мы не выводим столь же легко промежуточные положения из крайних. Следовательно, если теперь в не нарушаемом нигде порядке мы рассматриваем зависимость отдельных положений друг от друга, с тем чтобы отсюда вывести, каким образом последнее зависит от первого, то мы обозреваем затруднение прямо; напротив, если мы узнаем, что первое и последнее положения определенным образом связаны между собой, и вследствие этого пожелаем вывести, каковы промежуточные положения, которые их соединяют, то мы будем руководствоваться безусловно косвенным и обратным порядком. Поскольку же мы занимаемся здесь лишь темными вопросами, а именно теми, в которых на основании известных крайних терминов надо в обратном порядке познать некоторые промежуточные, то вся хитрость тут заключается в том, чтобы, допуская неизвестное в качестве известного, мы смогли в сколь угодно запутанных затруднениях представить себе легкий и прямой

147

путь их исследования. И ничто не мешает тому, чтобы так было всегда, ибо, как мы предположили с самого начала этой части, мы знаем, что зависимость тех терминов, которые в вопросе неизвестны, от известных такова, что первые полностью обусловлены последними. Так что если мы поразмыслим над теми самыми терминами, которые поначалу встретятся нам, когда мы признаем такую обусловленность, то, хотя мы и будем причислять эти неизвестные к известным, с тем чтобы постепенно посредством правильных рассуждений вывести из них и все остальные известные, как если бы они были неизвестными, мы выполним все то, что предписывает настоящее правило; примеры, поясняющие это и многое из того, что мы будем говорить в дальнейшем, мы откладываем до двадцать четвертого правила, так как удобнее изложить их там.

ПРАВИЛО XVIII

Для этого требуются только четыре действия: сложение, вычитание, умножение и деление; два последних здесь зачастую не следует производить, как для того, чтобы невзначай не запутать чего-нибудь, так и потому, что впоследствии они могут быть выполнены более легко.

Многочисленность правил часто проистекает из неопытности учителя, и то, что могло бы быть сведено к единому общему предписанию, становится менее очевидным, если разделяется на многие частности. Вот почему все действия, которыми нужно пользоваться при рассмотрении вопросов, т.е. при выведении каких-то величин из других, мы сводим здесь лишь к четырем главным; то, каким образом они оказываются достаточными, познается из их объяснения.

А именно, если мы приходим к познанию одной величины благодаря тому, что мы знаем части, из которых она составлена, это делается посредством сложения; если мы узнаём часть благодаря тому, что знаем целое и превышение целого над той же самой частью, это делается посредством вычитания; и какая-либо величина не может быть большим числом способов выведена из других, взятых в абсолютном смысле, величин, в которых она определенным образом содержится. Если же какая-либо величина должна быть найдена на основании других, от которых она совершенно отлична и в которых она никоим образом не содержится, необходимо соотнести ее с ними каким-нибудь способом; и когда это отношение, или соответствие, нужно обозреть прямо, тогда следует пользоваться умножением, когда косвенно - делением.

148

Чтобы ясно описать два последних действия, надо знать, что единица, о которой мы уже говорили, является здесь основанием и фундаментом всех отношений и в ряде непрерывно пропорциональных величин она занимает первую ступень, данные же величины содержатся на второй ступени, а искомые - на третьей, четвертой и остальных, если соотношение прямое, если же оно косвенное, искомая величина содержится на второй и других промежуточных ступенях, а данная - на последней.

Действительно, когда говорится, что, как единица относится к а, или к данному числу 5, так b, или данное число 7, относится к искомому, которое равно ab, или 35, тогда а и Ь находятся на второй ступени, и ab, являющееся их произведением, - на третьей. Равным образом, когда добавляют, что, как единица относится к с, или 9, так ab, или 35, относится к искомому аbс, или 315, тогда abc находится на четвертой ступени и получается посредством двух действий умножения ab на с, т.е. величин, находящихся на второй ступени, и т.д. Равным образом, как единица относится к а, (или) 5, так а, (или) 5, относится к а2, или 25; и опять-таки как единица относится к (а, или) 5, так а2, (или) 25, относится к а3, (или) 125; и, наконец, как единица относится к а, (или) 5, так а3, (или) 125, относится к а4, т.е. к 625, и т.д.: ведь когда одна и та же величина умножается на саму себя, умножение производится так же, как и тогда, когда она умножается на другую, совершенно отличную от нее величину.

Когда же теперь говорится, что, как единица относится к а, или 5, данному делителю, так В, или искомое число 7, относится к ab, или 35, данному делимому, тогда порядок является обратным и косвенным, вследствие чего искомое В не может быть получено иначе, кроме как посредством деления данного ab на а, также данное. Равным образом, когда говорится, что, как единица относится к А, или искомому числу 5, так А, или 5,искомое, относится к а2, или 25, данному; или же как единица относится к А, (или) 5, искомому, так А2, или 25, искомое, относится к а3, или 125, данному, и т.д. Все это мы охватываем названием "деление", хотя следует отметить, что последние из примеров такого вида заключают в себе большее затруднение, чем первые, ибо в них чаще встречается искомая величина, которая поэтому предполагает многие отношения. Ведь смысл этих примеров тот же самый, как если бы было

149

сказано, что надо извлечь квадратный корень из а , или <из> 25, либо кубический из а3, или из 125, и т.д.; такой способ выражения употребителен у счетчиков. Или, если объяснить их также в терминах геометров, это то же самое, как если бы было сказано, что надо найти среднюю пропорциональную между той принятой величиной, которую мы называем единицей, и той, которая обозначается а2, либо две средние пропорциональные между единицей и а3, и т.д.

Из этого легко сделать вывод о том, каким образом двух названных действий достаточно для отыскания любых величин, которые должны быть выведены из других величин благодаря какому-либо отношению. После того как мы поняли это, нам следует изложить, каким образом эти действия должны быть рассмотрены воображением и каким образом они должны также предстать перед глазами, для того чтобы затем мы наконец объяснили их использование, или применение.

Если нужно произвести сложение или вычитание, мы представляем себе предмет в виде линии или в виде протяженной величины, в которой должна быть рассмотрена только длина: действительно, если нужно прибавить линию

150

мы прикладываем одну линию к другой под прямым углом таким образом:

Наконец, при делении, в котором дан делитель, мы воображаем, что делимая величина представляет собой прямоугольник, одна сторона которого является делителем, а другая - частным; так, если прямоугольник ab нужно разделить на а,

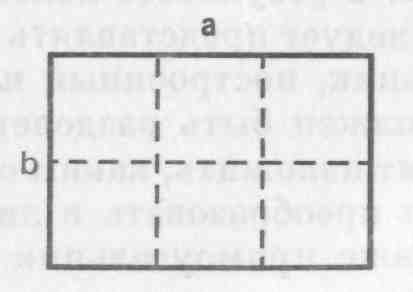
из него убирают ширину а, и остается b в качестве частного: . Или, наоборот, если тот же прямоугольник делят на b, то убирают высоту b, и а будет частным: .

Что же касается тех делений, в которых делитель не дан, а только обозначен через посредство какого-либо отношения, как, например, когда говорится, что нужно извлечь квадратный или кубический корень и т.д., то следует отметить, что в этих случаях и подлежащий делению, и все другие термины нужно всегда представлять себе как линии, расположенные в ряде непрерывно пропорциональных величин, первой из которых является единица, а последней - делимая величина. О том, каким образом между этой величиной и единицей должно быть найдено сколько угодно средних пропорциональных, будет сказано в своем месте. Теперь же достаточно уведомить, что здесь, как мы предполагаем, подобные действия еще не были доведены до совершенства, так как они должны производиться при посредстве непрямых и обратных актов воображения, а сейчас мы говорим только о вопросах, которые следует обозревать прямо.

Что касается других действий, то они, конечно, весьма легко могут быть осуществлены тем способом, которым, как мы сказали, их надлежит понимать. Вместе с тем остается изложить, каким образом должны быть подготовлены используемые в них термины; ибо, хотя, впервые занимаясь каким-либо затруднением, мы вольны представлять себе его термины как линии или как прямоугольники и никогда не приписывать этим терминам других фигур, как было сказано в четырнадцатом правиле, тем не менее в рассуждении часто бывает, что прямоугольник, после того как он был образован умножением двух линий, затем следует представлять себе в виде линии, для того чтобы выполнить другое действие, либо тот же самый прямоугольник или линию, полученную в результате какого-то сложения или вычитания, затем следует представлять себе как некоторый другой прямоугольник, построенный на обозначенной линии, которой он должен быть разделен.

152

Итак, здесь стоит изложить, каким образом всякий прямоугольник можно преобразовать в линию и в свою очередь линию или даже прямоугольник - в другой прямоугольник, сторона которого обозначена. Это весьма легко сделать геометрам, если только они заметят, что в виде линий, всякий раз когда мы, как здесь, сравниваем их с каким-либо прямоугольником, мы неизменно представляем себе прямоугольники, одна сторона которых является той длиной, какую мы приняли за единицу. Ведь тогда вся эта задача сводится к положению такого вида: по данному прямоугольнику построить другой, равный ему, на данной стороне.

Хотя это действие известно даже новичкам в геометрии, тем не менее мне хочется объяснить его, чтобы не показалось, будто я что-либо упустил.

ПРАВИЛО XIX

Посредством этого метода рассуждения нужно отыскивать столько величин, выраженных двумя различными способами, сколько неизвестных терминов мы допускаем в качестве известных, для того чтобы прямо обозреть затруднение; ибо таким образом мы будем иметь столько же сравнений между двумя равными терминами.

ПРАВИЛО XX

Отыскав уравнения, нужно произвести опущенные нами действия, ни в коем случае не пользуясь умножением тогда, когда будет уместно деление.

ПРАВИЛО XXI

Если имеется много таких уравнений, их все необходимо свести к одному, а именно к тому, члены которого займут меньшее число ступеней в ряде непрерывно пропорциональных величин, соответственно каковому они и должны быть расположены по порядку.

Конец

153